楞次定律

---

引言

最初，电和磁是两个独立的学科。电与电荷有关，磁与磁性材料有关。然而，在19世纪，丹麦物理学家奥斯特证明了这两者之间存在联系。他发现电流可以在其周围产生磁场。

英国实验科学家迈克尔·法拉第报道了一个有趣的现象。他发现，如果我们移动围绕连接到检流计的线圈的磁铁，我们会看到检流计的偏转。

在这种情况下，电路中电流的存在意味着当我们改变其周围的磁场时，会在电路中感应出电动势。这种现象称为电磁感应。感应电动势的大小由法拉第定律给出。它指出，磁通量的变化率等于电路中感应电动势。但是，如果我们想知道由于电磁感应而在电路中感应电流的方向，我们使用另一个定律。它被称为楞次定律。

什么是楞次定律？

1834年，俄罗斯物理学家埃米尔·楞次提出了一条帮助我们获得感应电流方向的定律。这就是著名的楞次定律。

它指出——如果在导体内部感应出电流，它也会在其周围产生磁场。电流的方向将是这样的：它产生的磁场将反对引起它的变化。为了更好地理解，让我们举个例子。

MikeRun, Lenzs-law-cylindrical-magnet-leaving-ring, CC BY-SA 4.0

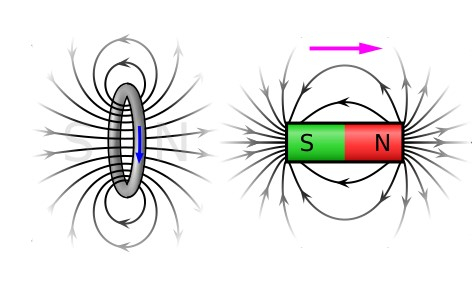
图1：楞次定律的图示

假设有一个如图所示的圆形导体。一根条形磁铁从左侧靠近它。移动的条形磁铁会在导体中感应出电流。我们可以看到，电流产生的磁场是顺时针方向的，而条形磁铁的原始磁场是逆时针方向的。因此，感应电流产生的磁场与感应电流的来源相反。

楞次定律的公式

楞次定律指出，电流或电动势将反对磁通量的变化，因为磁通量的变化是这种感应电动势的原因。如果磁场由B给出，磁通量为$\mathrm{\phi _{B}}$。那么

$$\mathrm{e=-N\frac{d\phi _{B}}{dt}}$$

N = 线圈数

dt = 时间变化量

这里的负号至关重要，因为它告诉我们方向。“反对”这个词包含在这个符号中。如果我们只需要感应电动势的大小，我们可以这样写

$$\mathrm{\left|e \right|\propto \frac{d\phi _{B}}{dt}}$$

什么是感应电动势？

当导体的磁通量发生变化时，会在其中感应出电动势。这被称为感应电动势。假设有一个N匝线圈，它在磁场中缓慢旋转，那么会在其中感应出电动势。感应电动势的大小可以用法拉第定律给出。如果磁场为B，并且通量dphi在时间dt内发生变化。则感应电动势

$$\mathrm{e =-N \frac{d\phi _{B}}{dt}}$$

楞次定律实验

楞次从理论上阐述了他的定律。他的理论通过以下三个实验得到了证实。

Keministi, Lenz law demonstration, CC0 1.0

第一个实验

在第一个实验中，当电流流过电路时，会在其周围产生磁场。当我们增加电流时，磁通量会增加，因为磁场取决于电流。电流会阻止磁通量的任何变化。

第二个实验

在第二个实验中，他发现，如果我们取一根载流导线并将其缠绕在铁棒上，则其一端表现为北极，并被磁铁的南极吸引。因此，会产生感应电流。

第三个实验

在第三个实验中，当线圈沿磁通量方向拖动时，线圈在磁场内的面积减小。楞次定律告诉我们，如果我们沿与线圈运动相反的方向施加感应电流，则线圈的运动会被阻止。

为此，磁场对线圈施加力。相反，线圈的电流对磁场施加磁力。

应用

它用于以下领域。

• 读卡器、麦克风和交流发电机。

• 它告诉我们电感器中储存的磁能。

• 这个概念用于金属探测器和列车的制动系统

• 它提供了对法拉第公式中负号的物理理解。

• 它用于涡流测功机和天平。

结论

电磁感应是一种现象，当磁通量变化时，会在导体中产生电动势。感应电动势的大小可以用法拉第定律给出。感应电动势或电流的方向由楞次定律给出。它指出感应电动势的方向是这样的：它会阻止磁通量中出现的任何变化。它在许多技术应用中非常有用。几乎在每一个使用电磁感应现象的地方都能看到它的重要性。

常见问题

Q1. 哪个守恒定律证明了楞次定律？

A1. 楞次定律是能量守恒定律（电能）的直接结果。

Q2. 线圈的磁通量由$\mathrm{\phi _{B}=B_{0}A\:sin\omega t}$给出，求感应电动势的表达式。

A2. 我们知道感应电动势为$\mathrm{e =-N \frac{d\phi _{B}}{dt}}$

$$\mathrm{e =-N \frac{d}{dt}(B_{0}A\:sin\omega t)=-NB_{0}A\:{\omega}cos(\omega t)}$$

Q3. 半径为10cm的圆环平行于磁场放置。磁场在200ms内从35mT变为60mT。求感应电动势的大小。

A3. 已知半径$\mathrm{r=10\times 10^{-2}m}$

此外，磁通量$\mathrm{\phi _{B}=B\pi r^{2}}$，因为B和A彼此平行。

$$\mathrm{感应电动势\:\left|e \right|=\frac{d}{dt}\phi _{B}=\frac{d}{dt}(B\pi r^{2})}$$

$$\mathrm{=\pi r^{2}\frac{dB}{dt}=\pi r^{2}\frac{(B_{2}-B_{1})}{t}}$$

$$\mathrm{\left|e \right|=\pi r^{2}\frac{25}{200}=\pi (10^{-2})(0.125)}$$

$$\mathrm{\left|e \right|=0.3925\times 10^{-2}V=3.9mV}$$

Q4. 对于感应电动势，磁场是否必须发生变化？

A4. 不，磁场并不总是需要变化。净磁通量应该变化。例如，可能存在磁场不变但面积矢量可能发生变化的情况。即使在这种情况下，我们也可以获得感应电动势。

Q5. 感应有哪些类型，简要描述。

A5. 感应可以分为两种类型

• 互感：在这种感应中，我们需要两个彼此靠近的线圈，一个线圈的磁通量变化会导致另一个线圈产生感应电动势。

• 自感：在这种感应中，我们只需要一个线圈。线圈本身会感应出电动势以阻止电流强度的变化。