波义耳定律

---

介绍

波义耳定律描述了压力对气体的影响，是现存的三条基本气体定律中最常用、影响最大的定律。因此，本教程将重点介绍它。潜水员使用水肺罐在水下作业和呼吸，就是一个简单的例子，它体现了波义耳定律在现实世界中的应用。

潜水员是如何在内容量通常小于百分之几立方英尺的水肺罐中长时间吸气保持潜水的呢？答案是，该罐被充压到 4000 到 5000 psig 之间。由于空气是可压缩的，因此在保持罐体体积不变的情况下，通过施加很大的压力，我们可以将大量空气“挤入”罐中。波义耳定律是一个计算压力变化引起体积变化的公式。

波义耳定律的表述

波义耳定律指出，如果我们取一定量的气体，并增加对其施加的压力，气体分子将更靠近地移动。此外，气体将占据更小的空间。

例如，天然气输配系统中管道系统的空间是固定的且恒定的。因此，提高系统压力也会提高通过管道网络输送的气体密度。

因此，波义耳定律的表述简化为

"在恒定温度下，理想气体的体积随着施加压力的增加而减小。"

波义耳定律的推导

波义耳定律指出，在恒定温度下，一定质量气体的体积 V 与其压力 p 成反比。

因此，我们可以很容易地写出，$\mathrm{V\:\varpropto\:\frac{1}{P}}$

或者，$\mathrm{PV = k_1}$

根据该公式，我们还可以写出 $\mathrm{P_1V_1 = P_2V_2}$

根据上述公式，初始体积和压力的乘积等于其中一个发生变化后（在恒温下）体积和压力的乘积。

波义耳定律的实验装置

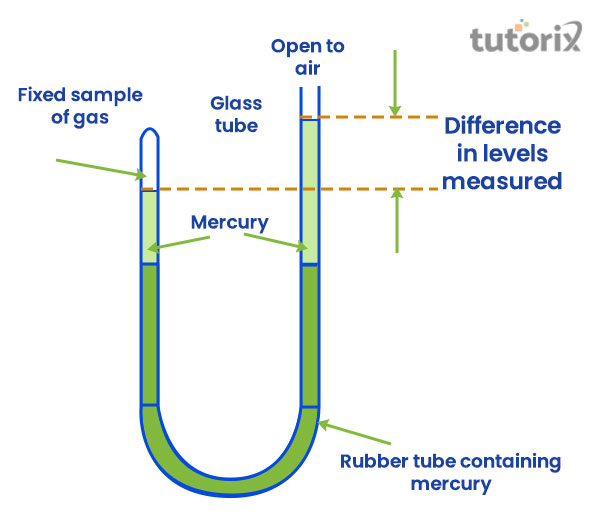
图中所示的装置用于进行实验以验证波义耳定律。通过升高或降低另一端，可以改变封闭端内气体（空气）的体积和压力。可以通过测量两根管中汞柱高度差来估计封闭端内气体的压力。假设玻璃管是圆柱体，则可以计算出该端气体的体积。

波义耳定律的数据分析

考虑下面所示与波义耳定律相对应的图表

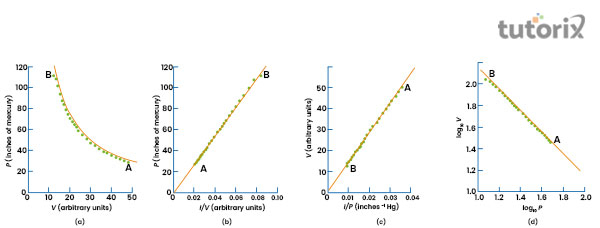
获得上述实验数据后，就可以尝试使用已测量的相互独立量来破译数学关系。其中一种方法可能是将不同量测量的各种幂相互绘制，以获得一条直线。直线的数学关系为

$$\mathrm{y\:=\:mx + c}$$

其中 m 和 c 是常数，而 x 和 y 是变量。在上图中，我们可以观察到 P 与 V 的关系图（图 (a))、P 与 1/V 的关系图（图 (b))、V 与 1/P 的关系图（图 (c)) 和 log V 与 log P 的关系图（图 (d))。P 与 1/V 的关系图（图 (b)) 和 V 与 1/P 的关系图（图 (c)) 给出了过原点的直线。log V 与 log P 的关系图也给出了一条直线，但其斜率为 -1。从这些图表中，我们可以推导出以下公式

$$\mathrm{P\:=\:\frac{m}{V}}$$

$$\mathrm{V\:=\:\frac{m}{P}}$$

$$\mathrm{以及,\:log\:V\:=\:log\:m\:-\:log\:P}$$

如果两个量之间的数学关系与建立波义耳定律的实验中测量的关系一样简单，则也可以用数值方法推导出它们。当 P 的值与 V 的对应值相乘时，对于特定气体在恒温下的乘积将近似一致。因此，从图表中我们可以很好地推导出

$$\mathrm{PV\:=\:m}$$

上述公式表示双曲线，它是通过绘制 P 和 V 得到的，如图 (a) 所示。

结论

本教程中讨论的气体定律是在近四个世纪前建立的，它们帮助科学家弄清楚如何在不同条件下计算气体的变量压力、体积和温度。罗伯特·波义耳在 1662 年发现了压力和体积之间的关系，假设温度恒定。如果温度保持恒定，则随着容器体积的膨胀，气体施加的压力将降低。

常见问题

Q1. 简述波义耳定律。

答：“在恒定温度下，对于特定气体分子给定数量的摩尔，气体的压力与其体积成反比。”

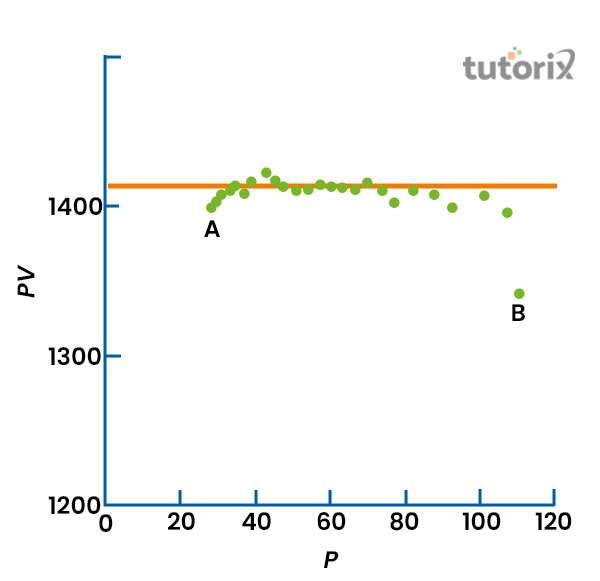
Q2. 对于服从波义耳定律的气体，PV 对 P 的关系图是什么样的？

答：根据波义耳定律，我们可以推导出特定气体在恒温下压力和体积的乘积是一个常数。因此，PV 对 P 的关系图将给出一条不过原点的水平直线。

Q3. 提到波义耳定律的一些现实生活中的应用。

答：波义耳定律的现实生活中的应用如下

(i) 我们都知道，吸气和呼气是呼吸或呼吸机制中的两个独立过程。因此，当我们吸气时，肺部体积增大，导致肺部内部压力与外部大气相比降低。结果，空气涌入肺部。

(ii) 当我们推动注射器的活塞时，筒体内液体的量减少，导致液体压力升高。结果，液体被输送到患者体内。

Q4. 写下波义耳定律的数学关系。

答：波义耳定律的数学公式可以表示为

$$\mathrm{V\:\varpropto\:\frac{1}{P}}$$

$$\mathrm{或者,\:PV\: =\: k_1}$$

其中，P = 气体压力，V = 气体体积，

$\mathrm{k_1}$ = 常数

Q5. 谁提出了波义耳定律？

答：波义耳定律是由英国自然哲学家罗伯特·波义耳提出的。