
Theano - 矩阵乘法表达式
我们将计算两个矩阵的点积。第一个矩阵的维度是 2 x 3,第二个矩阵的维度是 3 x 2。我们用作输入的矩阵及其乘积在此处表示 -
$$\begin{bmatrix}0 & -1 & 2\\4 & 11 & 2\end{bmatrix} \:\begin{bmatrix}3& -1 \\1 & 2 \\35 & 20 \end{bmatrix}=\begin{bmatrix}11 & 0 \\35 & 20 \end{bmatrix}$$声明变量
要为上述内容编写 Theano 表达式,我们首先声明两个变量来表示我们的矩阵,如下所示 -
a = tensor.dmatrix() b = tensor.dmatrix()
dmatrix 是双精度矩阵的类型。请注意,我们没有在任何地方指定矩阵大小。因此,这些变量可以表示任何维度的矩阵。
定义表达式
要计算点积,我们使用了名为 dot 的内置函数,如下所示 -
c = tensor.dot(a,b)
乘法的输出分配给一个名为 c 的矩阵变量。
定义 Theano 函数
接下来,我们像在前面示例中那样定义一个函数来计算表达式。
f = theano.function([a,b], c)
请注意,函数的输入是两个矩阵类型的变量 a 和 b。函数输出分配给变量 c,该变量将自动为矩阵类型。
调用 Theano 函数
我们现在使用以下语句调用函数 -
d = f([[0, -1, 2], [4, 11, 2]], [[3, -1],[1,2], [6,1]])
上述语句中的两个变量是 NumPy 数组。您可以像此处显示的那样显式定义 NumPy 数组 -
f(numpy.array([[0, -1, 2], [4, 11, 2]]), numpy.array([[3, -1],[1,2], [6,1]]))
计算 d 后,我们打印其值 -
print (d)
您将在输出上看到以下输出 -
[[11. 0.] [25. 20.]]
完整程序列表
The complete program listing is given here: from theano import * a = tensor.dmatrix() b = tensor.dmatrix() c = tensor.dot(a,b) f = theano.function([a,b], c) d = f([[0, -1, 2],[4, 11, 2]], [[3, -1],[1,2],[6,1]]) print (d)
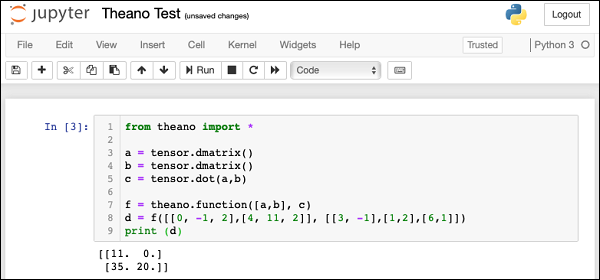
此处显示程序执行的屏幕截图 -
广告