通过绘制入射角和偏角之间的关系图，确定给定棱镜的最小偏角。

---

介绍

偏角是指光线通过两种不同折射率介质之间的界面时，出射光线与入射光线方向之间的夹角。当棱镜处于最小偏角位置时，第一表面上的入射角等于第二表面上的出射角。

目的

本实验旨在通过绘制入射角和偏角之间的关系图来确定棱镜的最小偏角。

所需材料

实验需要一些必备物品，包括画板、白纸（必不可少），整个过程都依赖于棱镜，因此需要一个棱镜 (Gao et al. 2018)。还有一些其他辅助仪器，例如大头针、铅笔、半米尺、图钉、量角器和坐标纸。

理论

出射光线偏离入射光线方向的角度称为偏角 d。另一方面，入射角是指入射方向与固体表面之间的夹角 (Gao et al. 2018)。

当光线从一种介质传播到另一种介质时，导致出射光线偏离入射光线，就会发生折射。棱镜中使用的材料的折射率为 -

$$\mathrm{n\:=\:\frac{[\frac{sin(A+Dm)}{2}]}{sin(\frac{A}{2})}}$$

其中 $\mathrm{D_m}$ 表示最小偏角，A 表示棱镜角。

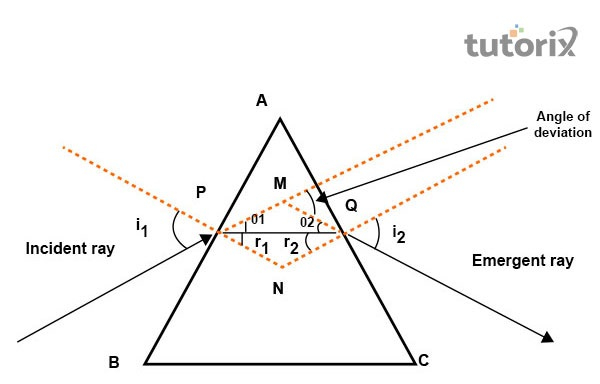
图 1：偏角

过程

• 首先，需要将一张白纸固定在画板上，可以使用图钉或胶带 (stackexchange, 2022)。

• 下一步，在纸的中间，保持适当的长度，画一条直线 XX'。为了测量完美的 5 厘米距离，需要在 XX' 线上标记点 Q1、Q2 和 Q3 (Nwosu&Egesi, 2021)。

• 下一步，根据图示，在 Q1、Q2、Q3 点上画出法线，例如 $\mathrm{N_1Q_1\: N_2Q_2 \:N_3Q_3}$。需要分别与法线成角画直线。

• 然后，将棱镜的角标记为 A，在所有观察中都应将其视为棱镜的边缘 (stackexchange, 2022)。

• 下一步，将 AB 线对准 XX' 线的顶部，并且在 AB 的中间，Q1 应为该点。应制作棱镜的边界。保持 10 毫米的距离，垂直固定两根或多根图钉在 $\mathrm{R_1Q_1}$ 线上。透过棱镜，面向 AC 并寻找点 $\mathrm{P_1}$ 和 $\mathrm{P_2}$ 的像。只睁开一只眼睛，使这两个像在一条线上。需要垂直固定另外两根图钉，就像图中所示。保持图钉之间的距离为 10 厘米是必须的。

• 然后，需要对点 $\mathrm{Q_2,\: Q_3}$ 和许多其他先前提到的过程重复执行。

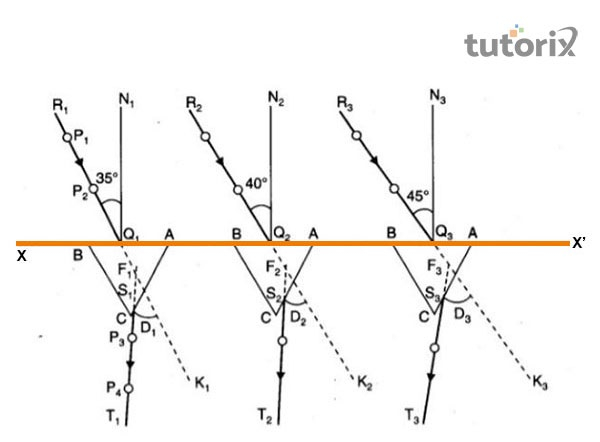
图 2：通过棱镜的折射

为了测量不同情况下的 D，以获得出射光线 $\mathrm{S_1T_1}$ 或更多，需要通过 $\mathrm{P_4}$ 和 $\mathrm{P_5}$ 画一条线 (Nwosu & Egesi, 2021)。为了与产生的入射光线相交，首先延长 $\mathrm{T_1S_1,\: S_2T_2}$ 等。需要测量该角度，从而得到偏角，并正确记录角度值 (learncbse, 2022)。另一方面，为了测量 A，应测量棱镜边界内的角 BAC。需要记录观察结果。

实验观察结果

棱镜角 A 等于：

序号	入射角 $\mathrm{\angle i}$	偏角 $\mathrm{\angle D}$
1	35°
2	40°
3	45°
4	50°
5	55°
6	60°

表 1：观察表

最终计算

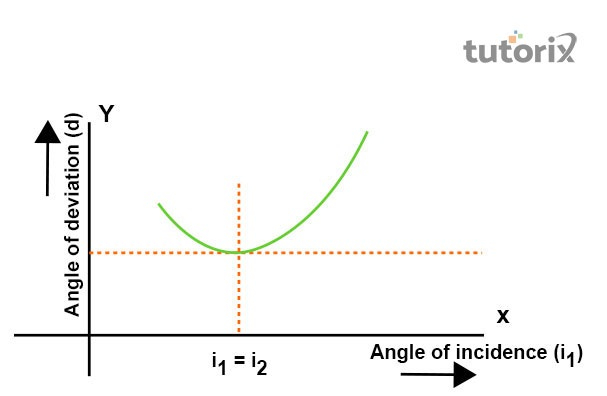
图 3：D 和 I 之间的关系图

绘制入射角和偏角之间的关系图，需要将 $\mathrm{\angle i}$ 放在 X 轴上，同样，需要将 $\mathrm{\angle D}$ 放在 Y 轴上 (learncbse, 2022)。只有从图中才能找到与最低点对应的 $\mathrm{D_m}$。

$\mathrm{D_m}$ 的值为 -

然后，$\mathrm{n\:=\:\frac{[\frac{sin(A+Dm)}{2}]}{sin(\frac{A}{2})}}$

最终结果

最小偏角为 -

然后，棱镜材料的折射率 n 将为

该图表明，入射角增加，然后偏角减小以达到 $\mathrm{D_m}$ 的值，最后随着 $\mathrm{\angle i}$ 的增加而增加。

结论

35 度到 60 度之间的角度是入射角，在整个过程中需要保持不变。图钉必须垂直放置，并且需要保持 10 毫米的距离。对于光线的表示，必须标记箭头。对于所有观察，棱镜角应保持相同。图钉扎出的孔可以足够粗，角度可能会测量错误。

常见问题

Q1. 什么是偏角？

A. 入射光线和出射光线方向之间的夹角称为偏角。

Q2. 什么是入射角？

A. 光线在表面上与入射方向之间形成的角度称为入射角。