利用图表求秒摆的有效长度

---

秒摆的有效长度是本实验的主要内容。实验将通过图表展示，L-T 和 L-T² 图有助于简单摆的计算。

目的

本实验的主要目的是利用单摆绘制 L-T² 图，并应用该图求出秒摆的有效长度。

所需仪器和材料

为了找到有效长度，需要一些材料和仪器。这些被认为是本次实验最重要的材料。材料包括：劈开的软木塞、铁架台、秒表、长而结实的棉线、铅笔橡皮、米尺、坐标纸和带钩的重金属球形摆锤。这些都是此应用过程中所需的材料。

原理

可以看出，利用图表求秒摆的有效长度具有一定的原理。该原理指出，单摆表现出简谐运动（SHM），因为摆锤的加速度与摆锤偏离平衡位置的位移成正比。这是因为摆锤的加速度与偏离平均位置的位移成正比，并且始终指向位移方向，并且这里通过使用其关系式展示了单摆的周期 (T)。

步骤

• 实验步骤包含以下几个步骤，第一步是将铁架台放置在桌子上。
• 然后，将摆锤上的钩子连接到一根长度为 150 厘米的线的末端（Cbselabs，2022）。
• 线的另一端应穿过两块劈开的软木塞的半片。
• 然后，将劈开的软木塞紧紧地夹在架子上，使软木塞与 OA 线垂直。在本实验中，必须注意使摆锤垂直悬挂，并使其悬挂在桌子边缘后面，以便它可以自由摆动。

在下图中，需要测量单摆的有效长度。然后，需要将摆锤的位移偏离 OA 垂直位置不超过 15 度的角度。

下一步，轻轻释放它，如果发现架子似乎不稳定，则需要在架子的底座上放置一个重物（Simo 等人，2019）。

在摆锤摆动时，需要注意到一些因素。例如，摆锤会绕其自身的轴旋转。在振荡期间，它不会上下移动。另一个需要注意的因素是，摆锤不会在其平均位置周围以椭圆路径旋转。使摆锤开始摆动后，需要等待几分钟。

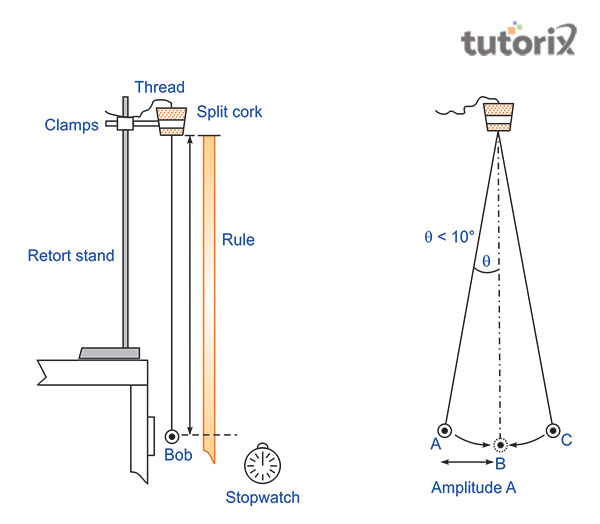
图 1：摆的有效长度

之后，当摆动完成时，开始下一步骤的秒表计时。摆锤经过平衡位置后，开始计数摆动次数 1、2、3。为了获得更好的结果，应该在计数到 n 次摆动时停止秒表。有时重复观察可以帮助记录相同的 n 次摆动次数 (Elkinany 等人，2020)。通过大约 10 厘米改变摆的长度可以帮助找到时间。如果使用表格形式记录观测结果，并使用有效数字和适当的单位，则观测结果会更好。

观察表格

序号	从摆锤顶部到悬挂点的线长	有效长度，L = (l+r+e)		计数的摆动次数，n	n 次摆动的时间 t (s)			周期 T (= t/n)
		厘米	米		(i)	(ii)	(iii)	平均 t (s)

表 1：周期计算

绘制图表

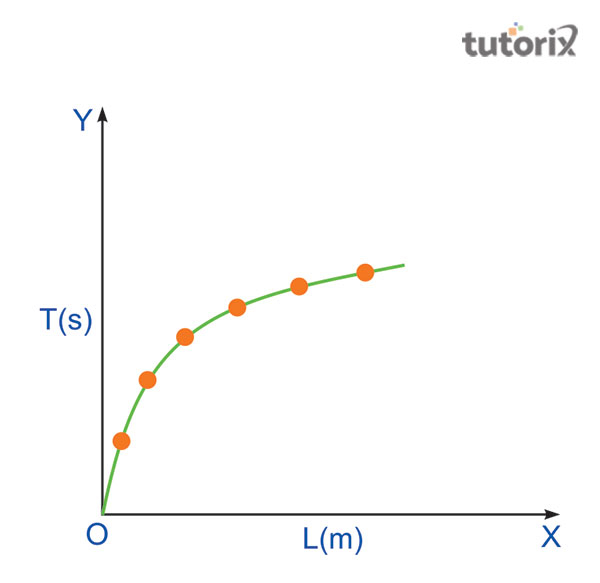
图 2：绘制图表 (L-T)

图 3：绘制图表 (L-T²)

(i) L 对 T 图

上表有助于记录 L 与 T 之间的图。这里 L 位于 x 轴上，T 位于 y 轴上。可以看出，根据图 1，该图是曲线，是抛物线的一部分。

(ii) L 对 T² 图

观察表还有助于记录 L 与 T² 之间的图。这里 L 位于 x 轴上，T² 位于 y 轴上。图 2 显示该图呈现一条穿过原点的直线。

结果

实验结果表明，L 对 T 图是曲线，并且向上凸。图 2 显示 L 对 T² 图绘制成一条直线。这里秒摆的有效长度用厘米测量。

注意事项

在本实验的这一部分中，需要注意一些注意事项。此处，线应牢固且不可伸长。悬挂点应由刚性支撑固定。摆锤在振动时不应旋转。

结论

本实验旨在利用两张图找到秒摆的有效长度。这里展示了这些图表，以便轻松讨论相关问题。使用摆实验可以非常有效地测量时间。本教程以简单的方式定义了相关问题。

常见问题解答

Q1. 什么是单摆？

单摆是一个单独的粒子，它由一根不可伸长的线和一根无重量的柔性线悬挂。这是借助无摩擦的支撑完成的。

Q2. 什么是简谐运动？

加速度的大小可以与位移建立正比关系。这称为简谐运动，并从平均位置显示。