查找有向图中长度为 K 的路径数

---

给定一个有向无权图 G 和一个整数 K。您必须找到图中长度为 K 的路径数。此处，图以邻接矩阵的形式给出。从顶点 i 到 j，如果存在边，则表示为 G[i][j]=1，否则表示为 G[i][j]=0。

输入

• 由邻接矩阵表示的有向无权图

• 表示要查找的路径长度的整数 K

输出

长度为 K 的路径总数

案例 I K=3

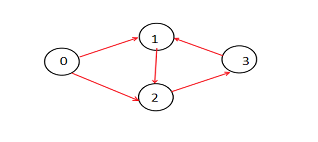
输出

路径总数= 2

解释

在上图中，有两条长度为 3 的路径。它们是-

• 0->1->2->3

• 0->2->3->1

案例 II K=2

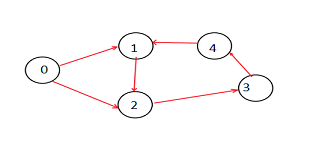
输出

路径总数 = 6

解释

在上图中，有两条长度为 3 的路径。它们是-

• 0->1->2

• 0->2->3

• 1->2->3

• 2->3->4

• 3->4->1

• 4->1->2

示例

import java.util.*;

public class Main {
   public static void main(String[] args) {
      int[][] G = {
         {0, 1, 1, 0},
         {0, 0, 1, 0},
         {0, 0, 0, 1},
         {0, 1, 0, 0}
      };
      int K = 3;
      List<List<Integer>> paths = fpath(G, K);
      
      System.out.println("Paths of length are");
      int count=0;
      for (List<Integer> path : paths) {
         count++;
         System.out.println(path);
      }
      System.out.println("Total number of paths "+count);
   }
   
   public static List<List<Integer>> fpath(int[][] G, int K) {
      List<List<Integer>> paths = new ArrayList<>();
      List<Integer> path = new ArrayList<>();
      boolean[] visited = new boolean[G.length];
      
      // Start the search from each vertex
      for (int i = 0; i < G.length; i++) {
         dfs(G, i, K, path, visited, paths);
      }
      
      return paths;
   }
   
   private static void dfs(int[][] G, int vertex, int K, 
List<Integer> path, boolean[] visited, 
List<List<Integer>> paths) {
      visited[vertex] = true;
      path.add(vertex);
      
      if (K == 0) {
         paths.add(new ArrayList<>(path));
      } else {
         for (int n = 0; n < G.length; n++) {
            if (G[vertex][n] == 1 && !visited[n]) {
               dfs(G, n, K - 1, path, visited, paths);
            }
         }
      }
      
      visited[vertex] = false;
      path.remove(path.size() - 1);
   }
}

输出

Paths of length are
[0, 1, 2, 3]
[0, 2, 3, 1]
Total number of paths 2

解释

为了找到长度等于 K 的路径，我们将使用 DFS（深度优先搜索）方法。有两个辅助函数 - fpath() 和 dfs()。

fpath() 函数

• 在 fpath() 函数中，邻接矩阵 G 和 K 作为参数传递。它返回一个包含列表作为路径的列表。此外，还打印了长度为 K 的路径总数。

• 初始化一个包含路径的列表列表，并初始化当前路径列表。创建一个布尔数组来标记已访问的顶点。为每个顶点调用 dfs() 方法，并检查它是否包含长度为 K 的路径。

dfs() 函数

• dfs() 函数用于执行深度优先搜索操作。它是一个递归函数。我们将传递图、当前顶点、剩余长度 K、已访问路径、一个跟踪已访问顶点的布尔数组 visited，以及“paths”（包含路径的列表列表）来存储路径。

• 在给定的 dfs() 函数中，我们将标记该顶点为已访问并将其添加到已访问路径中。现在访问相邻的顶点。如果相邻的顶点未被访问，则使用新顶点和剩余长度 K-1 递归调用 dfs() 函数。

• 如果 K 的值为 0，这是我们的基本情况，则当前已访问的路径将添加到“paths”中。否则，如果从顶点到邻居存在路径并且邻居未被访问，则递归调用该函数。

• 访问完所有邻居后，将顶点标记为未访问并将其从当前已访问路径列表中删除。这也被称为回溯。