使用 4:1 多路复用器的双变量函数

---

阅读本文，了解如何使用 4:1 多路复用器实现双变量布尔函数。让我们先简要介绍一下双变量布尔函数和多路复用器。

什么是双变量布尔函数？

双变量布尔函数是一个逻辑表达式，它有两个输入变量。其中，每个变量可以取二进制 0 或二进制 1 作为其值。双变量布尔函数可能有 4 种可能的变量组合，即在 SOP 形式中，$\bar{A}\bar{B},\bar{A} B,A \bar{B},AB,$ 最小项表示为 m₀, m₁, m₂ 和 m₃。在 POS 形式中，$(A+B),(A+\bar{B}),(\bar{A}+B),(\bar{A}+\bar{B})$ 最大项表示为 M₀, M₁, M₂, M₃。

什么是多路复用器？

在数字电子技术中，多路复用器，也称为MUX或数据选择器，是一种组合逻辑电路，它接收多个数据输入，并只允许其中一个数据输入一次通过输出线。多路复用器具有选择线，用于控制哪个数据输入将通过输出线。根据数据输入线的数量，有多种类型的多路复用器，例如 2:1 MUX、4:1 MUX、8:1 MUX、16:1 MUX 等。

4:1 多路复用器简介

4:1 多路复用器的框图如图 1 所示。

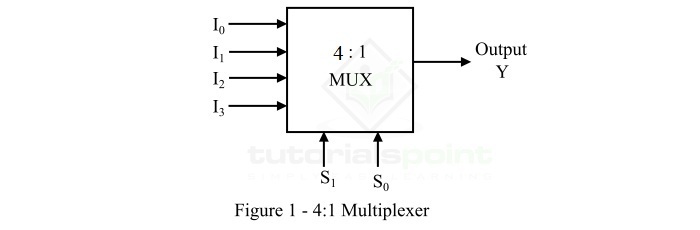
4:1 多路复用器由 4 条数据输入线，即 I₀、I₁、I₂ 和 I₃，以及两条选择线，即 S₀ 和 S₁ 组成。施加到 S₀ 和 S₁ 的逻辑电平决定哪个输入数据将通过输出线。

可以使用其真值表来理解 4:1 多路复用器的操作，如下所示。

选择线		输出
S1	S0	Y
0	0	I0
0	1	I1
1	0	I2
1	1	I3

众所周知，双变量布尔函数有 4 种可能的输入变量组合。因此，我们可以使用 4:1 多路复用器实现任何双变量布尔函数。

现在，让我们讨论使用 4:1 MUX 实现双变量布尔函数，并附带已解决的示例。

使用 4:1 多路复用器实现双变量函数

使用 4:1 多路复用器实现双变量布尔函数包括以下步骤：

• 步骤 1 - 绘制给定双变量布尔函数的真值表。

• 步骤 2 - 将两个输入变量 A 和 B 分别应用于选择线 S₁ 和 S₀。

• 步骤 3 - 将逻辑 1 连接到真值表中函数为 1 的那些数据输入线。

• 步骤 4 - 将逻辑 0 连接到所有剩余的数据输入线。

现在，让我们通过一个示例来了解使用 4:1 多路复用器实现双变量布尔函数。

示例 1

使用 4:1 多路复用器实现以下双变量逻辑函数。

$$F(A+B)=\sum m(0, 1, 3)$$

解答

给定逻辑函数的 4:1 多路复用器的真值表如下：

选择线		输出
S1 = A	S0 = B	Y
0	0	1
0	1	1
1	0	0
1	1	1

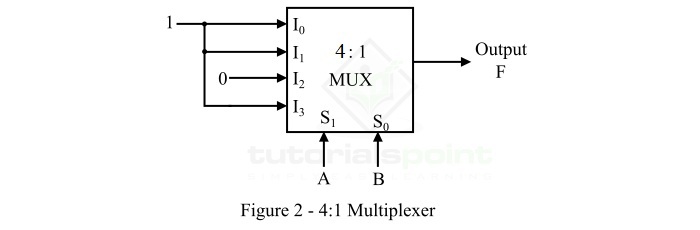
使用此真值表，我们可以绘制逻辑框图，以使用图 2 中所示的 4:1 MUX 实现函数 F。

解释

在这里，输入 A 和 B 分别应用于选择线 S₁ 和 S₀。从真值表可以清楚地看出，当 AB = 00、01、11 时，函数 F = 1。因此，我们将逻辑 1 连接到数据输入线 I₀、I₁ 和 I₃，并将逻辑 0 连接到数据输入线 I₂。

示例 2

使用 4:1 MUX 实现以下双变量逻辑函数。

$$F(A,B)=\sum m(1, 3)$$

解答

给定逻辑函数的 4:1 多路复用器的真值表如下：

选择线		输出
S1 = A	S0 = B	Y
0	0	0
0	1	1
1	0	0
1	1	1

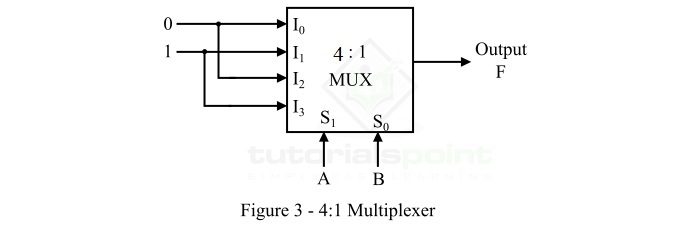
使用此真值表，我们可以绘制逻辑框图，以使用图 3 中所示的 4:1 MUX 实现函数 F。

解释

在这里，输入 A 和 B 分别应用于选择线 S₁ 和 S₀。从真值表可以清楚地看出，当 AB = 01、11 时，给定的布尔函数 F = 1。因此，我们将逻辑 1 连接到数据输入线 I₁ 和 I₃，并将逻辑 0 连接到其余的数据输入线，即 I₀ 和 I₂。

结论

通过这种方式，我们可以使用 4:1 多路复用器实现给定的双变量逻辑函数。尝试解决以下关于使用 4:1 多路复用器实现双变量布尔函数的教程问题，以便更深入地理解该概念。

问 1 - 使用 4:1 多路复用器实现以下双变量布尔函数。

$$F(x,y)=\sum m(0, 1)$$

问 2 - 使用 4:1 多路复用器实现以下双变量布尔函数。

$$F(A,B)=\sum m(1,2,3)$$

问 3 - 使用 4:1 MUX 实现以下布尔函数。

$$F(A,B)=\sum m(0)$$