数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究什么是左递归以及如何消除它？
一个文法 G (V, T, P, S) 如果它具有以下形式的产生式，则为左递归。
A → A α |β。
上述文法是左递归的，因为产生式的左侧出现在产生式右侧的第一个位置。可以通过用以下一对产生式替换它来消除左递归
A → βA′
A → αA′|ϵ
左递归的消除
可以通过引入新的非终结符 A 来消除左递归，使得。
这种类型的递归也称为**直接左递归**。
在左递归文法中，A 的展开将在每一步生成 Aα、Aαα、Aααα，导致它进入无限循环。
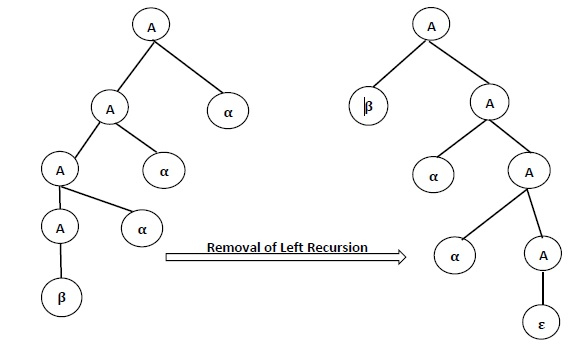
左递归的一般形式为
A → Aα1|Aα2| … . |Aαm|β1|β2| … . . βn
可以替换为
A → β1A′|β2A′| … . . | … . . |βnA′
A → α1A′|α2A′| … . . |αmA′|ε
**示例 1** − 考虑来自文法的左递归。
E → E + T|T
T → T * F|F
F → (E)|id
从文法中消除直接左递归。
解决方案
将 E → E + T|T 与 A → A α |β 进行比较
| E | → | E | +T | | | T |
| A | → | A | α | | | Β |
∴ A = E，α = +T，β = T
∴ A → A α |β 更改为 A → βA′ 和 A′ → α A′|ε
∴ A → βA′ 表示 E → TE′
A′ → α A′|ε 表示 E′ → +TE′|ε
将 T → T ∗ F|F 与 A → Aα|β 进行比较
| T | → | T | *F | | | F |
| A | → | A | α | | | β |
∴ A = T，α =∗ F，β = F
∴ A → β A′ 表示 T → FT′
A → α A′|ε 表示 T′ →* FT′|ε
产生式 F → (E)|id 没有左递归
∴ 组合产生式 1、2、3、4、5，我们得到
E → TE′ E′ → +TE′| ε T → FT′ T →* FT′|ε F → (E)| id
**示例 2** − 消除以下文法的左递归。
S → a|^|(T)
T → T, S|S
解决方案
在 T-产生式中存在直接左递归。
将 T → T, S|S 与 A → A α | β 进行比较，其中 A = T，α =, S，β = S
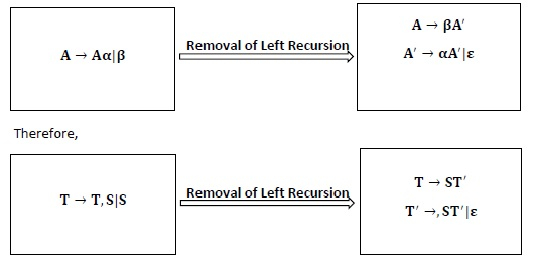
∴ 完整的文法将是
S→ a|^(T) T→ ST′ T′ →,ST′| ε
**示例 3** − 从文法中消除左递归
E → E + T|T
T → T * F|F
F → (E)|id
解决方案
去除左递归后的产生式将是
E → TE′ E′ → +TE′| ∈ T → FT′ T′ →∗ FT′| ∈ F → (E)|id
**示例 4** − 从文法中去除左递归
E → E(T)|T
T → T(F)|F
F → id
解决方案
消除所有 Aα 产生式中的直接左递归，我们得到
E → TE′ E → (T)E′|ε T → FT′ T′ → (F)T′|ε F → id
117K+ 次查看
