数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究在计算机体系结构中，二进制数的除法是什么？
二进制除法类似于十进制除法。该过程涉及连续比较、移位和减法。与十进制数的除法相比，二进制数的除法比较容易，因为商要么是 0 要么是 1。也没有必要检查被除数（部分余数）在除数中能容纳多少次。
除法溢出
在计算机系统中，除法运算可能导致商溢出，因为寄存器无法容纳超过标准长度的数字。为了更好地理解这一点，请考虑一个具有标准 5 位寄存器的系统。
一个寄存器用于保存除数，另一个寄存器用于保存被除数。如果商包含 6 位，则商的 5 位将存储在 5 位寄存器中。因此，溢出位需要一个触发器来存储第六位。
如果被除数的高位一半包含一个大于或等于除数的数字，则会发生除法溢出条件。在除法中需要考虑的另一点是，建议避免除以零。当触发器被置位时，通常会检测到溢出条件。这个触发器称为 DVF。
硬件算法
借助图表可以轻松解释硬件除法算法。该图显示了使用流程图的硬件除法算法。
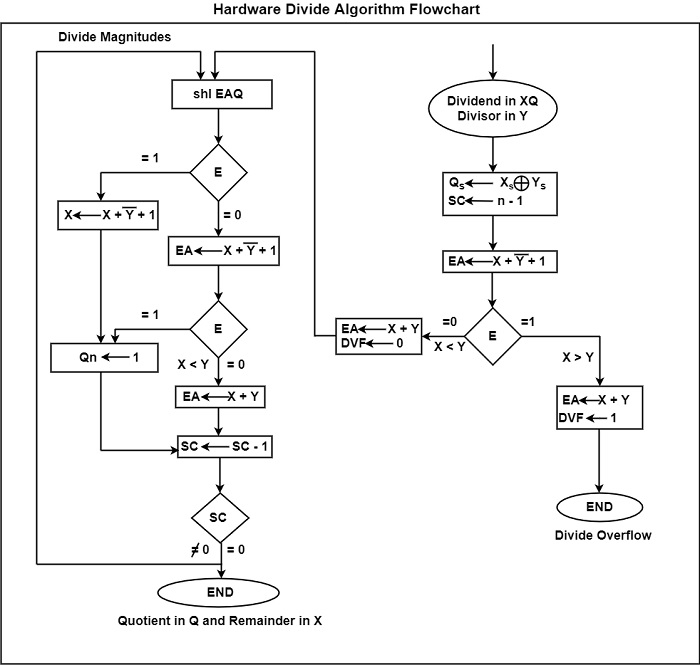
被除数在 X 和 Q 中，除数在 Y 中。结果的符号存储在 中，它是商的一部分。一个常数被设置为 SC 以确定商中的多位。
除法溢出条件的测试是通过从存储在 X 中的被除数的一半位中减去存在于 Y 中的除数来进行的。
- 在 XY 的情况下，DVF 被置位，并且操作会过早取消。
- 如果 X < Y，则不会发生除法溢出。因此，通过将 Y 加到 X 来恢复被除数的值。
幅值的除法从将存在于 XQ 中的被除数向左转移以及将高位转移到 E 开始。如果转移到 E 中的位是 1，则 EA > Y，因为 EA 包含一个 1 后跟 n - 1 位，而 Y 只包含 n - 1 位。
因此，从 EA 中减去 Y，并在 QS 中放置 1 作为商位。因为寄存器 X 没有被除数的高位，所以它的值为 EA - 2n−1。如果将 Y 的 2 的补码添加到此值，则输出将如下所示：-
(EA - 2n−1) + ( 22n−1 − Y) = EA − Y
如果 E 应该保持为 1，则来自加法的进位不应该转移到 E。
如果左移操作将 0 插入 E，则通过插入其 2 的补码值来减去除数。进位必须转移到 E。如果 E = 1，则表示 X Y，因此 QS 被设置为 1。如果 E = 0，则表示 X < Y，因此通过将 Y 加到 X 来恢复原始数字。在这种情况下，在移位期间插入的 0 保留在 QS 中。
3K+ 浏览量
