自动变压器启动器的工作原理

自动变压器启动器的电路和工作原理

图中显示了用于启动三相感应电动机的自动变压器启动器的电路图。自动变压器启动器可用于启动星形和三角形连接的三相感应电动机。在这种方法中，通过使用三相自动变压器降低初始施加到定子的电压来限制电动机的启动电流。自动变压器配备了许多分接头以获得可变电压。

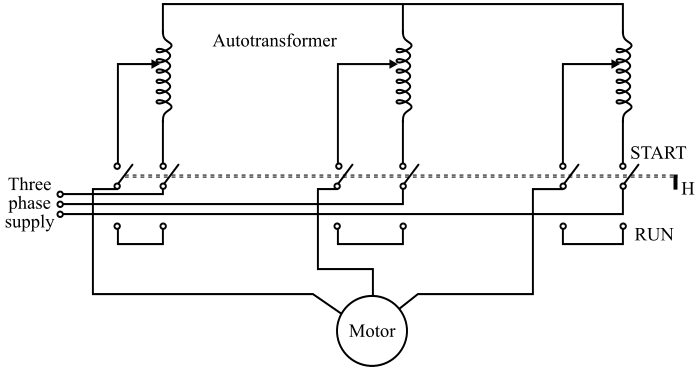
在自动变压器启动方法中，启动器连接到自动变压器的特定分接头上以获得最合适的启动电压。使用转换开关 S 将自动变压器连接到电路中以启动电动机。

当开关 S 的手柄 (H) 处于启动位置时，自动变压器的初级绕组连接到电源线，感应电动机连接到自动变压器的次级绕组。当电动机达到速度（约为额定速度的 80%）时，手柄 H 转换到运行位置。因此，自动变压器与电路隔离，电动机现在直接连接到电源线并获得其额定电压。欠压继电器将手柄保持在运行位置。当电源电压失效或低于某个值时，手柄释放并返回到关闭位置。为了对电动机提供过载保护，在电动机电路中使用热过载继电器。

自动变压器启动器的理论

下图显示了电动机直接切换和自动变压器启动电动机的电路连接。

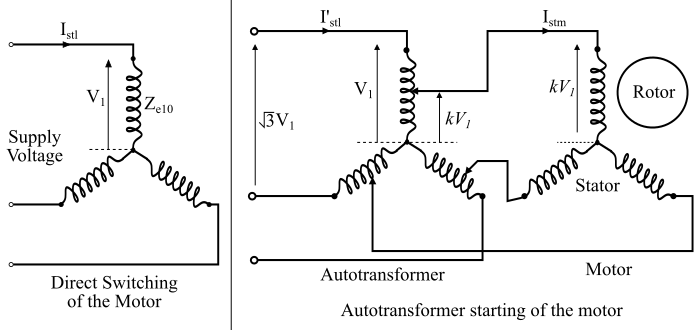
当电动机直接切换到电源线时 -

令，

𝑍_𝑒10 = 电动机在静止状态下折算到定子的每相等效阻抗

𝑉₁ = 每相电源电压

因此，当每相全电源电压 (V₁) 通过直接切换施加到电动机时，电动机从电源线汲取的启动线电流由下式给出：

$$\mathrm{𝐼_{𝑠𝑡𝑙} =\frac{𝑉_{1}}{𝑍_{𝑒10}}… (1)}$$

现在，使用自动变压器启动，如果使用变比为 k 的自动变压器分接头，则自动变压器次级绕组端子上的可用电压（即电动机上的每相电压）为 kV₁。因此，使用自动变压器启动的电动机的启动电流由下式给出：

$$\mathrm{𝐼_{𝑠𝑡𝑚} =\frac{𝑘𝑉_{1}}{𝑍_{𝑒10}}… (2)}$$

如果忽略变压器的空载电流，则变压器中的电流比与电压比成反比，即

$$\mathrm{\frac{𝐼_{1}}{𝐼_{2}}=\frac{𝑉_{2}}{𝑉_{1}}}$$

$$\mathrm{\Rightarrow\:𝑉_{1}𝐼_{1} = 𝑉_{2}𝐼_{2}}$$

因此，

$$\mathrm{𝑉_{1}{𝐼^{′}_{𝑠𝑡𝑙}} = 𝑘𝑉_{1}𝐼_{𝑠𝑡𝑚}}$$

其中，${𝐼^{′}_{𝑠𝑡𝑙}}$ 是自动变压器从电源汲取的线电流。

$$\mathrm{\Rightarrow 𝐼^{′}_{𝑠𝑡𝑙} = 𝑘𝐼_{𝑠𝑡𝑚} … (3)}$$

将式 (2) 中的 𝐼_𝑠𝑡𝑚 的值代入式 (3)，得到：

$$\mathrm{ 𝐼^{′}_{𝑠𝑡𝑙}=𝑘(\frac{𝑘𝑉_{1}}{𝑍_{𝑒10}})=\frac{𝑘^{2}𝑉_{1}}{𝑍_{𝑒10}}… (4)}$$

因此，

$$\mathrm{\frac{使用自动变压器启动器的启动电流\:(𝐼′_{𝑠𝑡𝑙} )}{使用直接切换的启动电流 \:(𝐼_{𝑠𝑡𝑙 })}=\frac{\frac{𝑘^{2}𝑉_{1}}{𝑍_{𝑒10}}}{\frac{𝑉_{1}}{𝑍_{𝑒10}}}= 𝑘^{2}}$$

$$\mathrm{\:因此；使用自动变压器启动器的启动电流= 𝑘^2\: × \:使用直接切换的启动电流 … (5)}$$

由于感应电动机中产生的转矩与施加电压的平方成正比。因此，使用直接切换的电动机的转矩为：

$$\mathrm{\tau_{𝑠𝑡𝑑} \propto 𝑉_{1}^{2} … (6)}$$

并且，使用自动变压器启动器产生的转矩为：

$$\mathrm{\tau_{𝑠𝑡𝑎} \propto 𝑘^2 𝑉_{1}^{2} … (7)}$$

因此，

$$\mathrm{\frac{使用自动变压器启动器的启动转矩 (\tau_{𝑠𝑡𝑎})}{使用直接切换的启动转矩 (𝐼_{𝑠𝑡𝑑})}=\frac{𝑘^2𝑉_{1}^{2}}{𝑉_{1}^{2}} = 𝑘^2}$$

$$\mathrm{\therefore\:使用自动变压器启动器的启动转矩\:=\:𝑘^2 × 使用直接切换的启动转矩 … (8)}$$

从式 (5) 和 (8) 可以清楚地看出，使用自动变压器启动器，电动机从主电源线汲取的启动电流和启动转矩分别降低到其使用电动机直接切换启动时的相应值的 k² 倍。

Manish Kumar Saini

更新于： 2021 年 8 月 27 日

12K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始