直接启动器(DOL)的工作原理

DOL启动器的接线图和工作原理

直接启动器(DOL)的连接图如图所示。在DOL启动笼型感应电动机的方法中，电动机通过启动器连接到全电压电源。

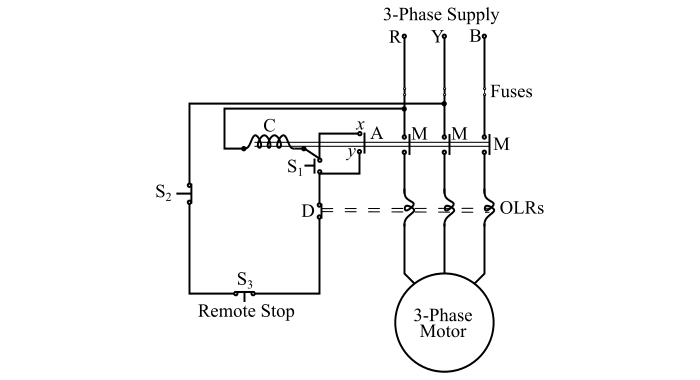
直接启动器由一个线圈控制的接触器C组成，该接触器由启动(常开)按钮和停止(常闭)按钮控制。

按下启动按钮(S₁)时，接触器线圈C从两条线R和Y获得能量。三个主触点(M)和辅助触点(A)闭合，端子x和y短路。因此，感应电动机连接到电源电压。

释放启动按钮时，它在弹簧的控制下返回。即使这样，接触器线圈C仍然通过端子x和y通电。因此，主触点(M)保持闭合，电动机继续获得电源电压。因此，辅助触点(A)也称为保持触点。

按下停止按钮(S₂)时，接触器线圈C的电源断开，因此接触器线圈C断电。结果，主触点(M)和辅助触点(A)打开。电动机的电源断开，因此电动机停止。

过载保护

当电动机发生过载时，过载继电器通电。常闭触点(D)打开，接触器线圈C断电以将电动机与电源断开。

熔断器连接在电路中，为电动机提供短路保护。

欠电压保护

当电动机端子上的电压降到一定值以下或电动机运行过程中电源发生故障时，接触器线圈C断电。因此，电动机与电源断开。

直接启动器是一种简单且成本较低的启动器，用于启动笼型感应电动机。对于此启动器，电动机所汲取的启动电流可能高达电动机额定电流的10倍，启动转矩等于额定转矩。因此，这种大的启动电流会在电动机连接的供电系统中产生过大的电压降。因此，为了避免电源电压波动，可以使用直接启动器启动功率高达5kW的小型电动机。

直接启动器的理论

设

• 𝐼_𝑠𝑡 = 电动机每相启动电流

  
  

• 𝐼_𝑓𝑙 = 电动机每相满载电流
• τ_𝑠𝑡 = 电动机启动转矩
• τ_𝑓𝑙 = 电动机满载转矩
• 𝑠_𝑓𝑙 = 对应于满载的滑差

现在，转子铜损耗由下式给出：

$$\mathrm{转子铜损 = 𝑠 \times 转子输入}$$

$$\mathrm{⇒ 3 𝐼_{2}^{2} 𝑅_2 = 𝑠 \times 2𝜋𝑛_𝑠\tau}$$

因此，电磁转矩为：

$$\mathrm{\tau =\frac{3 𝐼_{2}^{2} 𝑅_2 }{2𝜋𝑛_𝑠\tau}… (1)}$$

这里，n_s是同步速度(r.p.s.)。

在电动机启动时，𝑠 = 1；𝐼₂ = 𝐼_2𝑠𝑡；𝜏 = 𝜏_𝑠𝑡，则：

$$\mathrm{启动转矩, 𝜏_{𝑠𝑡} =\frac{3𝐼_{2𝑠𝑡}^{2} 𝑅_2}{2𝜋𝑛_𝑠}… (2)}$$

在满载时，𝑠 = 𝑠_𝑓𝑙；𝐼₂ = 𝐼_2𝑓𝑙；𝜏 = 𝜏_𝑓𝑙，则：

$$\mathrm{满载转矩, 𝜏_{𝑓𝑙} =\frac{3𝐼_{2𝑓𝑙}^{2} 𝑅_2}{2𝜋𝑛_𝑠𝑠_{𝑓𝑙}}… (3)}$$

因此，启动转矩与满载转矩之比为：

$$\mathrm{\frac{𝜏_{𝑠𝑡}}{𝜏_{𝑓𝑙}} = \frac{(\frac{3𝐼_{2𝑠𝑡}^{2} 𝑅_2}{2𝜋𝑛_𝑠})}{(\frac{3𝐼_{2𝑓𝑙}^{2} 𝑅_2}{2𝜋𝑛_𝑠𝑠_{𝑓𝑙}})}}$$

$$\mathrm{⇒\:\frac{𝜏_{𝑠𝑡}}{𝜏_{𝑓𝑙}} =(\frac{𝐼_{2𝑠𝑡}}{𝐼_{2𝑓𝑙}})^2\times𝑠_{𝑓𝑙} … (4)}$$

如果忽略电动机的空载电流，则：

$$\mathrm{\frac{有效定子匝数}{有效转子匝数}=\frac{𝐼_{2𝑠𝑡}}{𝐼_{𝑠𝑡}}}$$

此外：

$$\mathrm{\frac{有效定子匝数}{有效转子匝数}=\frac{𝐼_{2𝑓𝑙}}{𝐼_{𝑓𝑙}}}$$

$$\mathrm{\therefore\:\frac{𝐼_{2𝑓𝑙}}{𝐼_{𝑓𝑙}}=\frac{𝐼_{2𝑠𝑡}}{𝐼_{𝑠𝑡}}}$$

$$\mathrm{⇒\frac{𝐼_{𝑠𝑡}}{𝐼_{𝑓𝑙}}=\frac{𝐼_{2𝑠𝑡}}{𝐼_{2𝑓𝑙}}… (5)}$$

由方程(4)和(5)，我们得到：

$$\mathrm{\frac{𝜏_{𝑠𝑡}}{𝜏_{𝑓𝑙}}= (\frac{𝐼_{𝑠𝑡}}{𝐼_{𝑓𝑙}})^2 \times 𝑠_{𝑓𝑙} … (6)}$$

现在，如果V₁是每相等效定子电压，Z_e10是参考到定子的电动机每相阻抗处于静止状态，则启动电流为：

$$\mathrm{𝐼_{𝑠𝑡} =\frac{𝑉_1}{𝑍_{𝑒10}}= 𝐼_{𝑠𝑐} … (7)}$$

因此，启动电流等于电动机的短路电流。由方程(6)和(7)，我们有：

$$\mathrm{\frac{𝜏_{𝑠𝑡}}{𝜏_{𝑓𝑙}}= (\frac{𝐼_{𝑠𝑐}}{𝐼_{𝑓𝑙}})^2\times 𝑠_{𝑓𝑙} … (8)}$$

Saini Manish Kumar

更新于：2021年8月25日

15K+ 浏览量

开启您的职业生涯

完成课程获得认证

开始学习