星三角启动器的工作原理

星三角启动器的电路图和工作原理

该图显示了三相异步电动机与星三角启动器的连接图。星三角启动器是一种非常常见的启动器，广泛用于启动鼠笼式异步电动机。它用于启动设计为在三角形连接定子绕组上正常运行的鼠笼式异步电动机。

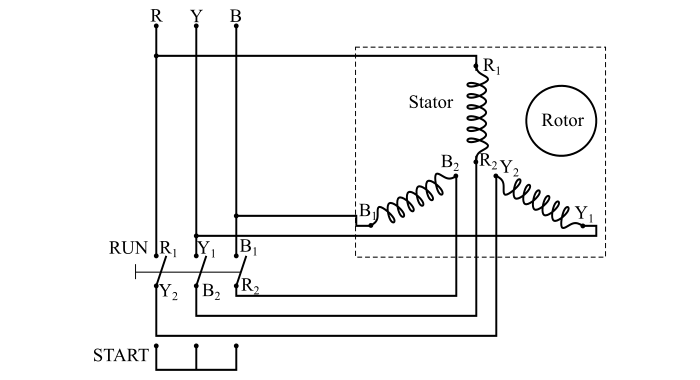
当开关 S 处于 START 位置时，定子绕组星形连接。当电机达到额定速度的约 80% 时，切换开关 S 切换到 RUN 位置，将定子绕组三角形连接。

通过首先将定子绕组星形连接，然后三角形连接，启动时电机吸收的线路电流减少到三角形连接绕组启动电流的三分之一。在启动时，当定子绕组星形连接时，每个相位获得的电压等于 𝑉_𝐿/√3，其中 V_L 是线电压。

由于异步电动机的转矩与施加电压的平方成正比，因此与直接三角形启动获得的转矩相比，星三角启动器将启动转矩降低到三分之一。

星三角启动器的理论

在启动时，定子绕组以星形方式连接，因此每个相绕组上的电压为

$$\mathrm{𝑉_1 =\frac{𝑉_𝐿}{\sqrt{3}}}$$

其中，

• V_L = 线电压
• V₁ = 定子相电压

假设，

𝐼_{𝑠𝑡.𝑌.𝑝ℎ} = 定子绕组星形连接时的每相启动电流

𝐼_{𝑠𝑡.𝑌.𝐿} = 定子绕组星形连接时的启动线电流

此外，对于星形连接，线电流等于相电流，即

$$\mathrm{𝐼_{𝑠𝑡.𝑌.𝐿} = 𝐼_{𝑠𝑡.𝑌.𝑝ℎ}}$$

同样，

𝐼_{𝑠𝑡.∆.𝑝ℎ} = 定子绕组三角形连接时的每相启动电流

𝐼_{𝑠𝑡.∆.𝐿} = 定子绕组三角形连接时的启动线电流

𝐼_{𝑠𝑐.∆.𝑝ℎ} = 定子绕组三角形连接时的短路相电流

𝑍_𝑒10 = 电机在静止状态下折算到定子的每相等效阻抗

因此，定子绕组星形连接时的每相启动电流由下式给出：

$$\mathrm{𝐼_{𝑠𝑡.𝑌.𝑝ℎ} =\frac{𝑉_1}{𝑍_{𝑒10}}=\frac{𝑉_𝐿}{\sqrt{3} 𝑍𝑒10}… (1)}$$

而定子绕组三角形连接时的每相启动电流为

$$\mathrm{𝐼_{𝑠𝑡.∆.𝑝ℎ} =\frac{𝑉_𝐿}{𝑍_{𝑒10}}… (2)}$$

对于三角形连接，

$$\mathrm{线电流 = \sqrt{3} × 相电流}$$

$$\mathrm{⇒ 𝐼_{𝑠𝑡.∆.𝐿} = \sqrt{3} × 𝐼_{𝑠𝑡.∆.𝑝ℎ} =\frac{\sqrt{3} × 𝑉_𝐿}{𝑍_{𝑒10}}… (3)}$$

现在，取星三角启动的启动线电流与直接三角形切换的启动线电流之比为

$$\mathrm{\frac{𝐼_{𝑠𝑡.𝑌.𝐿}}{𝐼_{𝑠𝑡.∆.𝐿}}=\frac{𝐼_{𝑠𝑡.𝑌.𝑝ℎ}}{𝐼_{𝑠𝑡.∆.𝐿}}=\frac{(𝑉_𝐿/\sqrt{3}𝑍_{𝑒10})}{\sqrt{3}(𝑉_𝐿/𝑍_{𝑒10})}=\frac{1}{3}}$$

⇒ 𝐼_{𝑠𝑡.𝑌.𝐿} = 𝐼_{𝑠𝑡.𝑌.𝑝ℎ} =\frac{1}{3}× 𝐼_{𝑠𝑡.∆.𝐿} … (4)

因此，使用星三角启动器，来自主电源的启动电流是直接三角形切换时启动电流的三分之一。

此外，

$$\mathrm{\frac{Y − ∆ 启动器的启动转矩}{直接三角形切换的启动转矩} =\frac{(𝑉_𝐿/\sqrt{3})^2}{𝑉_𝐿^2} =\frac{1}{3}… (5)}$$

因此，使用星三角启动，启动转矩降低到直接三角形切换获得的启动转矩的三分之一。

Manish Kumar Saini

更新于： 2021年8月28日

22K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

立即开始