数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学C/C++ 中的 2-3 树（搜索和插入）？
2-3 树定义为一种树形数据结构，其中每个具有子节点的内部节点要么有两个子节点（2-节点）和一个数据元素，要么有三个子节点（3-节点）和两个数据元素。
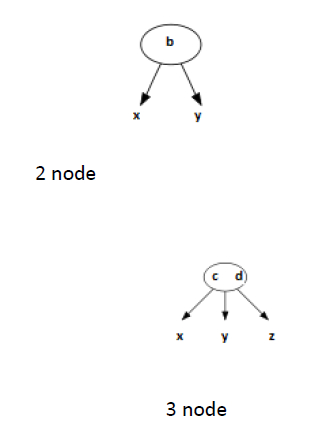
定义
如果一个内部节点具有一个数据元素和两个子节点，则称其为 2-节点。
如果一个内部节点具有两个数据元素和三个子节点，则称其为 3-节点。
当且仅当以下语句之一满足时，我们称 T 为 2-3 树：
T 为空。换句话说，T 不包含任何节点。
T 是一个具有数据元素 a 的 2-节点。如果 T 具有左子节点 L 和右子节点 R，则我们得出结论：
L 和 R 被视为相同高度的非空 2-3 树；
a 大于 L 中的每个元素；并且
a 小于或等于 R 中的每个数据元素。
T 是一个具有数据元素 a 和 b 的 3-节点，其中 a 小于 b。如果 T 具有左子节点 L、中间子节点 M 和右子节点 R，则我们得出结论：
L、M 和 R 被视为相同高度的非空 2-3 树；
a 大于 L 中的每个数据元素且小于或等于 M 中的每个数据元素；并且
b 大于 M 中的每个数据元素且小于或等于 R 中的每个数据元素。
属性
每个内部节点都被视为 2-节点或 3-节点。
所有叶子节点都位于同一层。
所有数据都保持排序。
操作
搜索
在 2-3 树中搜索项目与在二叉搜索树中搜索项目相同。由于每个节点中的数据元素都是有序的，因此搜索函数将被引导到正确的子树，最终到达包含该项目的正确节点。
设 T 为 2-3 树，d 为我们要查找的数据元素。如果 T 为空，则 d 不在 T 中，我们完成操作。
设 r 为 T 的根节点。
设 r 为叶子节点。如果 d 不在 r 中，则 d 不在 T 中。否则，d 在 T 中。特别是，d 可以在叶子节点中找到。我们不需要进一步步骤，操作完成。
假设 r 是一个具有左子节点 L 和右子节点 R 的 2-节点。设 e 为 r 中的数据元素。
有三种情况：
如果 d 等于 e，则我们在 T 中找到 d，操作完成。
如果 d 小于 e，则将 T 设置为 L（根据定义，L 是一个 2-3 树），并返回步骤 2。
如果 d 大于 e，则将 T 设置为 R，并返回步骤 2。
假设 r 是一个具有左子节点 L、中间子节点 M 和右子节点 R 的 3-节点。设 a 和 b 为 r 的两个数据元素，其中 a
如果 d 等于 a 或 b，则 d 在 T 中，操作完成。
如果 d 小于 a，则将 T 设置为 L，并返回步骤 2。
如果 a 小于 d 且 d 小于 b，则将 T 设置为 M，并返回步骤 2。
如果 d 大于 b，则将 T 设置为 R，并返回步骤 2。
插入
插入通过搜索键的正确位置并将其添加到该位置来执行。如果节点变成 4-节点，则该节点将被分成两个 2-节点，中间键将被移动到父节点。然后父节点可能会变成 4-节点，在这种情况下，它也会被分割，并将键传播到其父节点。此过程重复进行，直到我们到达不需要分割的 2-节点父节点，或者到达根节点，在这种情况下，我们将传播的元素实现为创建一个新的 2-节点根节点。借助此算法，执行的操作数量与树的高度成正比，因此由于树是完全平衡的，所以是对数级的。此过程确保其结果为 2-3 树：特别是，所有叶子节点都保持在相同的深度。
下图解释了此过程的可能情况。
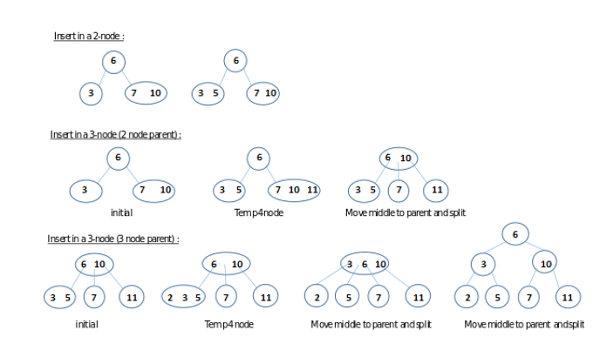
在 2-3 树中插入数字的 3 种可能情况。
668 次浏览
