摊销分析\n
摊销分析
在偶尔出现的操作非常慢,而大多数执行非常频繁的操作更快的情况下,使用此分析。我们需要摊销分析的数据结构为哈希表、分离集合等。
在哈希表中,搜索时间复杂度大多数时候为 O(1),但有时它会执行 O(n) 操作。当我们想在哈希表中搜索或插入一个元素时,大多数情况下,它会用常量时间执行任务,但当发生冲突时,它需要 O(n) 次操作来解决冲突。
聚合方法
聚合方法用于查找总成本。如果我们要添加一组数据,那么我们需要使用此公式找出摊销成本。
对于 n 个操作的序列,成本为−

摊销分析示例
对于一个动态数组,可以在给定的下标中以 O(1) 时间插入项。但如果该下标不在数组中,它就无法在常量时间内执行任务。对于这种情况,它最初将数组大小加倍,然后在存在下标时插入该元素。
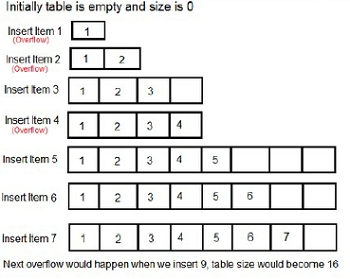
对于动态数组,让 c_i = 第 _i_ 次插入的成本。
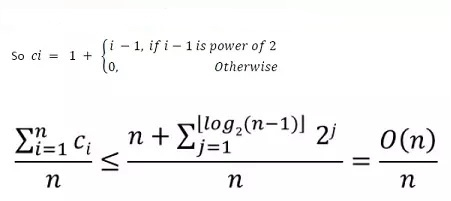

广告

 数据结构
数据结构 网络
网络 RDBMS
RDBMS 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP