Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies图中的桥
如果移除某个无向图中的边之后，会使该图断开连接或变成不同的组成部分，则该边被称为桥。
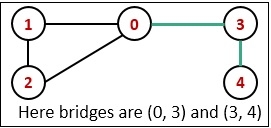
实际情况下，如果某网络中存在桥，当桥连接中断后，则会破坏整个网络。
输入和输出
Input: The adjacency matrix of the graph. 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 1 0 0 0 1 0 Output: Bridges in given graph: Bridge 3--4 Bridge 0--3
算法
bridgeFind(start, visited, disc, low, parent)
输入 − 起始顶点，标记节点已访问的 visited 数组，disc 将记录顶点的发现时间，low 将记录有关子树的信息。parent 将记录当前顶点的父顶点。
输出 − 如果发现任何桥则打印。
Begin time := 0 //the value of time will not be initialized for next function calls mark start as visited set disc[start] := time+1 and low[start] := time + 1 time := time + 1 for all vertex v in the graph G, do if there is an edge between (start, v), then if v is visited, then parent[v] := start bridgeFind(v, visited, disc, low, parent) low[start] := minimum of low[start] and low[v] if low[v] > disc[start], then display bridges from start to v else if v is not the parent of start, then low[start] := minimum of low[start] and disc[v] done End
示例
#include<iostream>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{1, 0, 0, 0, 1},
{0, 0, 0, 1, 0}
};
int min(int a, int b) {
return (a<b)?a:b;
}
void bridgeFind(int start, bool visited[], int disc[], int low[], int parent[]) {
static int time = 0;
visited[start] = true; //make the first vertex is visited
disc[start] = low[start] = ++time; //initialize discovery time and the low time
for(int v = 0; v<NODE; v++) {
if(graph[start][v]) { //for all vertex v, which is connected with start
if(!visited[v]) {
parent[v] = start; //make start node as parent
bridgeFind(v, visited, disc, low, parent);
low[start] = min(low[start], low[v]); //when subtree from v is connected to one of parent of start node
if(low[v] > disc[start])
cout << "Bridge " << start << "--"<<v<<endl;
} else if(v != parent[start]) //update low of start for previous call
low[start] = min(low[start], disc[v]);
}
}
}
bool bridges() {
bool *vis = new bool[NODE];
int *disc = new int[NODE];
int *low = new int[NODE];
int *parent = new int[NODE];
for(int i = 0; i<NODE; i++) {
vis[i] = false; //no node is visited
parent[i] = -1; //initially there is no parent for any node
}
for(int i = 0; i<NODE; i++)
if(!vis[i]) //if any node is unvisited, the graph is not connected
bridgeFind(i, vis, disc, low, parent);
}
int main() {
cout << "Bridges in given graph:"<<endl;
bridges();
}输出
Bridges in given graph: Bridge 3--4 Bridge 0--3
更新日期：16-Jun-2020
超过 2K 次浏览
广告