数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会研究
时尚研究
法律研究费用最小多边形三角剖分
如果多边形中不相交的对角线形成三角形，则称为三角剖分。我们的任务是找到三角剖分的最小成本。
三角剖分的成本是其组成三角形的权重之和。我们可以通过相加三角形的边来找到每个三角形的权重，换句话说，权重是三角形的周长。
输入和输出
Input:
The points of a polygon. {(0, 0), (1, 0), (2, 1), (1, 2), (0, 2)}
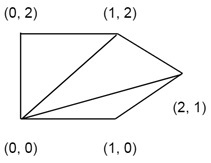Output:
The total cost of the triangulation. Here the cost of the triangulation is 15.3006.算法
minCost(polygon, n)
下面将使用 cost() 来计算三角形的周长。
输入：一套构成多边形的点以及点的数量。
输出 −多边形三角剖分的最小成本。
Begin if n < 3, then return 0 define table or order n x n i := 0 for gap := 0 to n-1, do for j := gap to n-1, do if j < i+2, then table[i,j] := 0 else table[i, j] = ∞ for k := i+1 to j-1, do val := table[i, k] + table[k, j] + cost(i, j, k) if table[i, j] > val table[i, j] := val i := i + 1 done done return table[0, n-1] End
示例
#include <iostream>
#include <cmath>
#include <iomanip>
#define MAX 1000000.0
using namespace std;
struct Point {
int x, y;
};
double min(double x, double y) {
return (x <= y)? x : y;
}
double dist(Point p1, Point p2) { //find distance from p1 to p2
return sqrt(pow((p1.x-p2.x),2) + pow((p1.y-p2.y),2));
}
double cost(Point triangle[], int i, int j, int k) {
Point p1 = triangle[i], p2 = triangle[j], p3 = triangle[k];
return dist(p1, p2) + dist(p2, p3) + dist(p3, p1); //the perimeter of the triangle
}
double minimumCost(Point polygon[], int n) {
if (n < 3) //when polygon has less than 3 points
return 0;
double table[n][n];
for (int gap = 0; gap < n; gap++) {
for (int i = 0, j = gap; j < n; i++, j++) {
if (j < i+2)
table[i][j] = 0.0;
else {
table[i][j] = MAX;
for (int k = i+1; k < j; k++) {
double val = table[i][k] + table[k][j] + cost(polygon,i,j,k);
if (table[i][j] > val)
table[i][j] = val; //update table data to minimum value
}
}
}
}
return table[0][n-1];
}
int main() {
Point points[] = {{0, 0}, {1, 0}, {2, 1}, {1, 2}, {0, 2}};
int n = 5;
cout <<"The minimumcost: " <<minimumCost(points, n);
}输出
The minimumcost: 15.3006
更新于： 17-6-2020
665 浏览量
广告