长度测量：三角测量和视差法

---

引言

测量是将未知量与已知值进行比较的过程。测量是一个测量系统。测量总是数值化的。测量包括长度、质量、体积、温度等。它与几何、三角学、代数等相关。测得的值被赋予单位。长度、质量和时间的基本单位分别是米(m)、千克(kg)和秒(sec)。测量长度的方法有很多。但是，恒星之间的距离和太空物体之间的距离是用三角测量和视差法测量的。

什么是长度三角测量法？

恒星之间的距离是用三角测量和视差法计算的。三角测量法指的是三角形三个要素的要求。这个过程是找到用于计算太空物体距离或位置的三个要素。它不仅被天文学家使用，也被测量员和建筑师使用。如果任何物体的位 置或距离未知，则可以使用此三角测量法通过考虑三角形的另两个点来找到该位置。

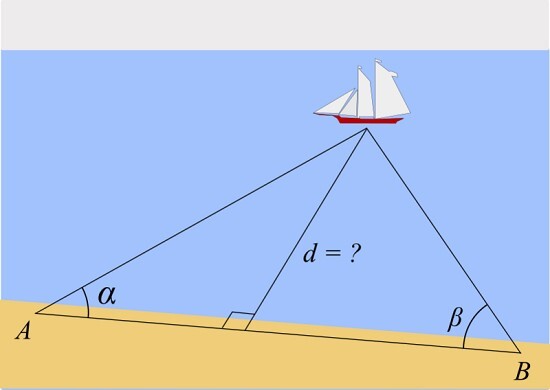
在海岸线上考虑两点作为三角形的基线。第三个点是海上的船，距离未知。连接点A和C的线与基线成α角。同样，连接点B和C的线与基线成β角。这些角是从海岸线到海上的船形成的。由于我们知道基线距离和两个角，因此可以计算出船与海岸线的距离。

船到海岸线的距离由下式给出：

$$\mathrm{d\:=\:l\:\frac{\sin\alpha\sin\beta}{\sin(\alpha+\beta)}}$$

l表示A和B之间的距离。

长度三角测量法的例子

通常，三角形形状足够坚固且刚性。因此，三角测量法用于建筑物和结构的建造，因为它是最强形式。这种三角测量法用于寻找船到海岸线的距离。

什么是视差法？

让我们伸出一只手指，指向你眼睛前方离脸部很近的地方。现在闭上左眼，用右眼看手指，反之亦然。不断这样做，手指的位置看起来不同，看起来像从一个地方跳到另一个地方。这就是视差效应。从两个不同的点观察图像的视觉之间存在明显的位移。视差法利用三角测量法的原理来测量距离。大多数天文学家都使用视差法，从中受益匪浅。当乘坐车辆行驶时，我们可以看到离我们较近的车辆看起来行驶速度很快。远处 的车辆看起来行驶速度很慢。

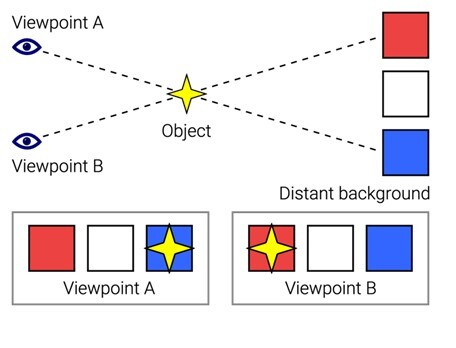
视差法利用三角测量法来找到恒星之间的距离或太空物体之间的距离。恒星之间的距离以秒差距为单位测量。

让我们考虑从地球上的两点观察到的遥远物体，以及遥远物体与基线AB之间的距离d。那么视差角的倒数就是距离。视差角的单位是角秒。

$$\mathrm{d\:=\:\frac{1}{\theta}\:秒差距}$$

视差法的例子

在摩托车的仪表板上，有一个指针式速度计。它显示车辆的速度。由于人们观察仪表的位置不同，它对不同的人来说看起来也不同。驾驶员注意到某种速度。但是，由于视线的角度，对于后面的人来说，相同的仪表显示不同的读数。

长度三角测量法和视差法的区别

三角测量法通过地球上的精确基线来测量物体的距离。它用于建筑施工和测量。视差法利用三角形的原理来利用角度和距离之间的三角关系。天文学家使用它来测量距离。

已解决的例子

例1

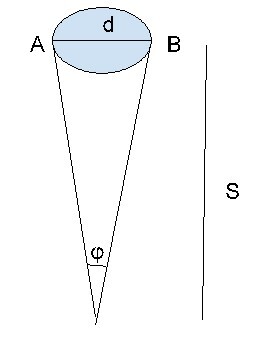
根据多普勒效应，土星和离地球较近的卫星之间的距离为1.5107 x 109公里，根据天文台的信息，土星所张开的角度为77 x 10-3弧度。求土星的直径。

已知 − $\mathrm{S\:=\:1.5107\:\times\:10^{9}km\:\varphi\:=\:77\times\:10^{-3}rad}$

现在基线是土星的直径，所以有两点，第三点在卫星上。那么土星的直径是

$$\mathrm{d\:=\:S\varphi}$$

$$\mathrm{d\:=\:1.5107\times\:10^{9}\:\times\:77\times\:10^{-3}rad}$$

$$\mathrm{d\:=\:116.3239\:\times\:10^{6}km}$$

结论

在本教程中，讨论了长度三角测量法及其示例。还讨论了视差法和视差法的示例。还讨论了三角测量法和视差法的区别。

常见问题解答

1. 秒差距是什么意思？

秒差距用于表示大距离的长度单位。特别是对于位于太阳系之外的天文物体。它是1个天文单位与1角秒的比率。1秒差距的值约为3.26光年或206 x 103天文单位。

2. 视差法的局限性是什么？

• 如果视差角小于0.01角秒，则很难找到距离。

• 视差法的一个缺点是使用三角学。

• 计算器并不总是精确的。

3. 视差法中作出的主要近似是什么？

与地球上某点到行星的距离相比，地球上两点之间的距离非常小。

4. 视差法可以用于测量遥远恒星的距离吗？

不可能找到遥远恒星的距离。因为在非常远的距离上，视差角太小，无法精确找到。

5. 什么是立体视差？

如果从不同的角度观察图像，则会发生相移。类似地，从不同方面的参考中拍摄同一物体的照片图像称为立体视差。相邻照片的重叠称为立体像对。