在 JavaScript 树中删除节点

树是一种非线性数据结构，它包含节点和边；其中边充当两个节点之间的链接，节点在其内部保存值。

遍历是一种过程，它将检索树中每个节点的数据并按指定的顺序打印它们。

下面列出了三种类型的树遍历：

  • 中序遍历 - 中序技术将遵循路径(左 → 根 → 右)。

  • 前序遍历 - 前序技术将遵循路径(根 → 左 → 右)。

  • 后序遍历 - 后序技术将遵循路径(左 → 右 → 根)。

从树中删除节点

从树中删除节点这个术语基本上是一个过程，在这个过程中，一个节点被删除并形成一个新的形状。但在某些其他情况下，它会消除它们之间的链接，并替换为树中的其他节点。

通常，内存（存储）中不会有任何树状结构。它们是内存中随机放置的元素（节点），我们试图借助指针（边）将它们连接起来。

如果我们需要删除一个元素，需要分离附加到它的指针并将其分配给相应的元素。

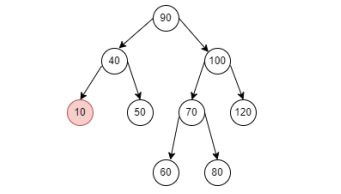
考虑下面的示例：

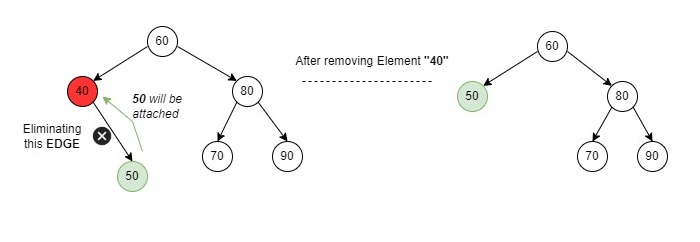
在上述情况下，我们尝试删除一个节点(40)，该节点附加了一个子节点。如果要删除的节点只有一个子节点，它将复制该子节点到该节点并删除该子节点。

可以从树中删除节点。其中有三种可能的删除节点的情况。以下列出了这些情况。

场景 1 - 如果要删除的节点是叶子节点，则在这种情况下可以将其简单地从树中删除。

算法

如果节点是叶子节点

  • 从树中删除节点。

场景 2 - 如果要删除的节点只有一个子节点，它将复制其子节点到该节点并删除该子节点。

算法

如果节点有一个子节点

  • 找到它的子节点，假设为 c_node。
  • 将其设置为 node → data = c_node。
  • 再次删除子节点。

场景 3 - 如果要删除的节点有两个子节点。

  • 首先，找到节点的中序后继，并将它的值复制到要删除的节点，然后删除中序后继节点。

算法

如果节点同时具有左子节点和右子节点

  • 在右子树中找到最小的节点，假设为 min_node。
  • 将其设置为 node → data = min_node。
  • 再次删除 min_node。

示例

在下面的示例中，我们实现了一个二叉搜索树，并在其中插入了足够数量的节点。我们对给定的树执行了删除操作。我们还在从树中删除选定节点后执行了中序遍历。

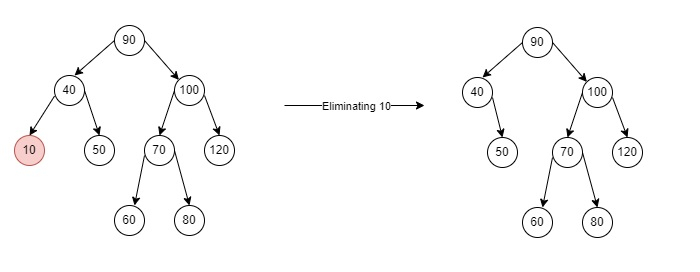
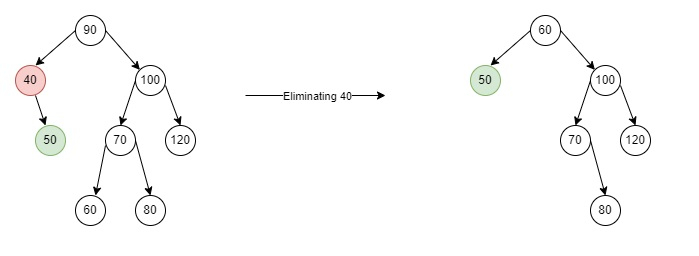
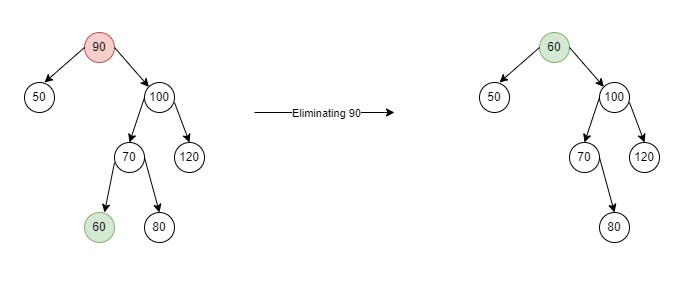
<!DOCTYPE html>
<html>
   <head>
      <script>
         class Node {
            constructor(item) {
               this.key = item;
               this.left = this.right = null;
            }
         }

         let root = null;
         function deleteKey(key) {
            root = deleteRecursive(root, key);
         }
         function deleteRecursive(root, key) {
            if (root == null)
               return root;
            if (key < root.key)
               root.left = deleteRecursive(root.left, key);
            else if (key > root.key)
               root.right = deleteRecursive(root.right, key);
            else {
               if (root.left == null)
                  return root.right;
               else if (root.right == null)
                  return root.left;
               root.key = minimumValue(root.right);
               root.right = deleteRecursive(root.right, root.key);
            }
            return root;
         }
         function minimumValue(root) {
            let minValue = root.key;
            while (root.left != null) {
               minValue = root.left.key;
               root = root.left;
            }
            return minValue;
         }
         function insert(key) {
            root = insertRec(root, key);
         }
         function insertRec(root, key) {
            if (root == null) {
               root = new Node(key);
               return root;
            }
            if (key < root.key)
               root.left = insertRec(root.left, key);
            else if (key > root.key)
               root.right = insertRec(root.right, key);
            return root;
         }
         function inorder() {
            InorderRecursion(root);
         }
         function InorderRecursion(root) {
            if (root != null) {
               InorderRecursion(root.left);
               document.write(root.key + " ");
               InorderRecursion(root.right);
            }
         }
         insert(90);
         insert(40);
         insert(10);
         insert(50);
         insert(100);
         insert(70);
         insert(60);
         insert(80);
         insert(120);
         document.write("After inserting the above nodes In-order will be: <br>");
         inorder();
         document.write("<br>Delete the node 10<br><br>");
         deleteKey(10);
         document.write("In-order after node 10 is deleted from the tree <br>");
         inorder();
         document.write("<br>Delete the node 40<br><br>");
         deleteKey(40);
         document.write("In-order after node 40 is deleted from the tree <br>");
         inorder();
         document.write("<br>Delete the node 90<br><br>");
         deleteKey(90);
         document.write("After removing the above nodes, the In-order will be as follows: <br>");
         inorder();
      </script>
   </head>
   <body>
   </body>
</html>

输出

上述脚本的输出将是：

After inserting the above nodes In-order will be:
10 40 50 60 70 80 90 100 120

Delete the node 10

In-order after node 10 is deleted from the tree
40 50 60 70 80 90 100 120

Delete the node 40

In-order after node 40 is deleted from the tree
50 60 70 80 90 100 120

Delete the node 90

After removing the above nodes, the In-order will be as follows:
50 60 70 80 100 120

更新于: 2022-11-18

2K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告

© . All rights reserved.