C++程序：用深度替换二叉树中的节点

假设我们有一个二叉树，我们希望用每个节点的深度替换其值。节点的深度从根节点的0开始，每向下遍历一层增加1；例如，我们有一个这样的二叉树；


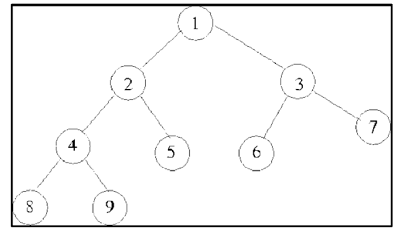
这里我们替换，

节点值 深度
1 0
2 1
3 1
4 2
5 2
6 2
7 2
8 3
9 3

我们进行简单的先序遍历，并将每个节点赋予深度。

让我们看一些输入场景 -

假设二叉树中节点的值为 [3 2 7 5 4 6 9 7 2]，从该输入获得的输出将为 -

Input: [3 2 7 5 4 6 9 7 2]
Result:
Before: 6 5 9 2 4 3 7 7 2
After: 3 2 3 1 2 0 2 1 2

假设二叉树中节点的值为 [4 3 5 6 10 7 12 8 1]，从该输入获得的输出将为 -

Input: [4 3 5 6 10 7 12 8 1]
Result:
Before: 7 6 12 3 10 4 8 5 1
After: 3 2 3 1 2 0 2 1 2

示例

下面是一个 C++ 程序，用于用二叉树中节点对应的深度替换二叉树中的节点值 -

#include <iostream>
using namespace std;
class Node {
   public:
   int value;
   Node *left, *right;
   Node(int value) {
      this->value = value;
      left = right = NULL;
   }
};
void solve(Node *node, int depth) {
   if (node == NULL) {
      return;
   }
   node->value = depth;
   solve(node->left, depth+1);
   solve(node->right, depth+1);
}
void printInorder(Node* root) {
   if (root == NULL) {
      return;
   }
   printInorder(root->left);
   cout << root->value <<" ";
   printInorder(root->right);
}
int main() {
   Node* root = new Node(1);
   root->left = new Node(2);
   root->right = new Node(3);
   root->left->left = new Node(4);
   root->left->right = new Node(5);
   root->left->left->left = new Node(8);
   root->left->left->right = new Node(9);
   root->right->left = new Node(6);
   root->right->right = new Node(7);
   cout << "Before: ";
   printInorder(root);
   solve(root, 0);
   cout << "\nAfter: ";
   printInorder(root);
   return 0;
}

输出

Before: 8 4 9 2 5 1 6 3 7
After: 3 2 3 1 2 0 2 1 2

结论

我们得出结论，使用树的简单先序遍历并在每个节点处用深度替换值足以解决问题。时间复杂度为 O(n)。这是一篇我们希望对您有所帮助的文章。

更新于: 2022年8月10日

287 次查看

开启你的 职业生涯

通过完成课程获得认证

立即开始
广告