放大器增益 – 功能、问题与解决方案

放大器的功能

放大器用于增强或放大微弱信号。中继器是放大设备的典型例子。根据发射器和接收器之间的实际距离，它们会以少量到多个的数量存在于发射器和接收器之间的中间点。在发射器和接收器之间的中间站进行周期性放大，确保信号具有所需的信噪比 (SNR)，以便成功完成最终传输。

理解放大器增益

示例 1

在一个由两个级联串联的放大器组成的系统中，第一个放大器的增益为 10 dB，第二个放大器的增益为 15 dB，那么相对于第一个放大器的输入信号，第二个放大器输出端的总信号放大倍数是多少？

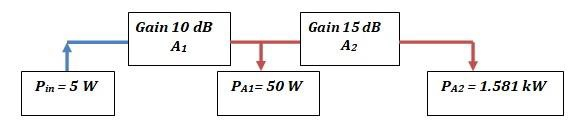
方法

已知输入信号功率为 5 W。我们知道，线性比例上的乘法在对数比例上变成了加法。我们还知道，对于这样的级联放大器系统，如果考虑其线性比例的值，则其总增益是各个放大器增益的乘积。当我们将这些线性比例的值转换为对数比例时，我们可以将各个放大器的增益相加，以得到放大器系统的总增益。加法比乘法更容易执行，因此增益以 dB 表示，以便可以通过简单地将各个放大器提供的增益相加来计算最终增益。

$$功率增益(dB)=10log_{10}(\frac{P_{out}}{P_{ref}})=10log_{10}(\frac{P_{out}}{P_{in}})=10log_{10}(\frac{P_{A1}}{P_{in}})$$

$$10dB=10log_{10}(\frac{P_{A1}}{P_{in}})=10log_{10}(\frac{P_{A1}}{5W})$$

$$10log_{10}(\frac{P_{A1}}{5W})=\frac{10}{10}=1$$

$$(\frac{P_{A1}}{5W})=10^{1}=10\Rightarrow\:P_{A1}=(10)(5W)=50W$$

可以看出，第一个放大器输出端的信号功率级别为 50 W，是输入信号功率的 10 倍。因此，放大系数为 10，这也对应于输入功率级别增加了 10 dB。因此，我们可以说，功率级别增加 10 dB 对应于具有最初可用功率的十倍。

输入功率增加 10 dB ⇒ 将输入功率乘以 10

让我们讨论第二级放大。第一个放大器的输出功率为 50 W。我们知道第二个放大器设计为提供 15 dB 的增益。那么最终的输出功率级别是多少？我们遵循相同的程序。唯一的区别在于用其新值（计算为 50 W）替换初始输入功率或参考功率的值。

$$15dB=10log_{10}(\frac{P_{A2}}{P_{A1}})=10log_{10}(\frac{P_{A2}}{50W})$$

$$log_{10}(\frac{P_{A2}}{50W})=\frac{15}{10}=1.5$$

$$(\frac{P_{A2}}{50W})=10^{1.5}\sim\:31.622\Rightarrow\:P_{A2}=(31.622)(50W)=1581.13W\sim\:1.581kW$$

我们可以观察到，第一个放大器的输出功率级别放大了约 31.622 倍，从而使我们获得 1.581 kW 的最终输出功率。

该系统的总放大倍数是多少？答案是 316.22，转换为 25 dB。

$$总增益=(10)(31.622)=316.22\equiv25dB=10dB+15dB$$

$$25dB=10log_{10}(\frac{P_{A2}}{P_{in}})$$

$$log_{10}(\frac{P_{A2}}{P_{in}})=2.5\Rightarrow\:(\frac{P_{A2}}{P_{in}})=10^{2.5}\sim\:316.22$$

示例 2

让我们考虑一个处理电压增益而不是功率增益的示例。这里进行电压放大。让我们继续使用相同的放大器系统和相同的放大值。

一个重要的事实是功率与电压的平方成正比。

$$P=\frac{V^{2}}{R}$$

$$P(dB)=\frac{V^{2}}{R}(dB)$$

$$10log_{10}P=10log_{10}(\frac{V^{2}}{R})$$

考虑单位电阻，我们有

$$10log_{10}P=10log_{10}(V^{2})=20log_{10}V$$

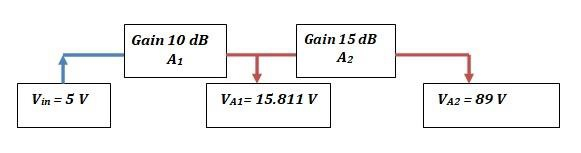
让我们找到 V_A1 和 V_A2 的值。

$$电压增益(dB)=20log_{10}(\frac{V_{out}}{V_{ref}})=20log_{10}(\frac{V_{out}}{V_{in}})=20log_{10}(\frac{V_{A1}}{V_{in}})$$

$$10dB=20log_{10}(\frac{V_{A1}}{V_{in}})=20log_{10}(\frac{V_{A1}}{5V})$$

$$log_{10}(\frac{V_{A1}}{5V})=\frac{10}{20}=0.5$$

$$(\frac{V_{A1}}{5V})=10^{0.5}=3.162;\:V_{A1}=15.811V$$

输入电压增加 10 dB ⇒ 将输入电压乘以 √10

同样地，

输入电压增加 20 dB ⇒ 将输入电压乘以 10

我们现在计算 V_A2。输入电压现在为 15.811 V。

$$15dB=20log_{10}(\frac{V_{A2}}{V_{A1}})=20log_{10}(\frac{V_{A2}}{15.811V})$$

$$log_{10}(\frac{V_{A2}}{15.811V})=\frac{15}{20}=0.75$$

$$(\frac{V_{A2}}{15.811V})=10^{0.75}=5.623;\:V_{A2}\sim\:89V$$

$$总增益=(3.162)(5.623)=17.8\equiv25dB=10dB+15dB$$

$$25dB=20log_{10}(\frac{P_{A2}}{P_{in}})$$

$$10log_{10}(\frac{P_{A2}}{P_{in}})=1.25\Rightarrow\:(\frac{P_{A2}}{P_{in}})=10^{1.25}\sim\:17.8$$

我们还可以注意到，将功率级别提高 3 dB 等效于将最初可用的功率加倍。

快速提示

如果放大器提供 3 dB 的功率放大，则表示放大器输出端的功率是其初始值的二倍。

如果放大器提供 6 dB 的电压放大，则表示放大器输出端的电压是其初始值的二倍。

S. Venkataraman

更新于：2021年6月23日

524 次浏览

启动您的职业生涯

完成课程获得认证

开始