Apache MXNet - Python 包

上一页
下一页

在本章中，我们将学习 Apache MXNet 中可用的 Python 包。

重要的 MXNet Python 包

MXNet 具有以下重要的 Python 包，我们将逐一讨论：

  • Autograd（自动微分）

  • NDArray

  • KVStore

  • Gluon

  • 可视化

首先让我们从 Apache MXNet 的Autograd Python 包开始。

Autograd

Autograd 代表自动微分，用于将梯度从损失度量反向传播回每个参数。除了反向传播之外，它还使用动态规划方法来有效地计算梯度。它也称为反向模式自动微分。此技术在“扇入”情况下非常有效，在“扇入”情况下，许多参数会影响单个损失度量。

什么是梯度？

梯度是神经网络训练过程的基础。它们基本上告诉我们如何改变网络的参数以提高其性能。

众所周知，神经网络 (NN) 由算子组成，例如求和、乘积、卷积等。这些算子在其计算中使用参数，例如卷积核中的权重。我们必须找到这些参数的最优值，而梯度则向我们展示了方法，并引导我们找到解决方案。

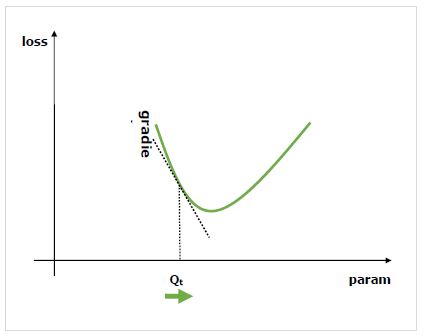
Graph_of_Gradients

我们对改变参数对网络性能的影响感兴趣，梯度告诉我们，当我们改变一个变量时，给定变量增加或减少多少，它取决于。性能通常使用我们尝试最小化的损失度量来定义。例如，对于回归，我们可能会尝试最小化预测值和精确值之间的L2损失，而对于分类，我们可能会最小化交叉熵损失。

一旦我们计算出每个参数相对于损失的梯度，我们就可以使用优化器（例如随机梯度下降）。

如何计算梯度？

我们有以下选项来计算梯度：

  • 符号微分 - 第一个选项是符号微分，它计算每个梯度的公式。此方法的缺点是，随着网络变得更深以及算子变得更复杂，它将很快导致难以置信的长公式。

  • 有限差分 - 另一个选项是使用有限差分，它尝试对每个参数进行轻微的差异，并观察损失度量如何响应。此方法的缺点是，它在计算上会很昂贵，并且可能具有较差的数值精度。

  • 自动微分 - 上述方法缺点的解决方案是使用自动微分将梯度从损失度量反向传播回每个参数。传播允许我们使用动态规划方法来有效地计算梯度。此方法也称为反向模式自动微分。

自动微分 (autograd)

在这里，我们将详细了解 autograd 的工作原理。它基本上分以下两个阶段工作：

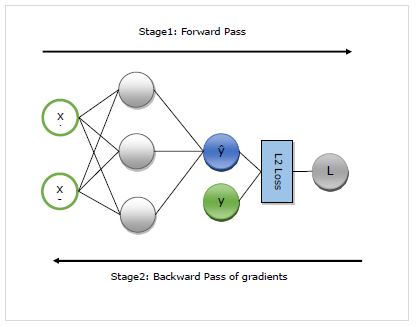
阶段 1 - 此阶段称为训练的“前向传递”。顾名思义，在此阶段，它会创建网络用于进行预测和计算损失度量的算子的记录。

阶段 2 - 此阶段称为训练的“后向传递”。顾名思义，在此阶段，它会通过此记录向后工作。向后移动，它会评估每个算子的偏导数，一直回到网络参数。

Automatic Differentiation

autograd 的优势

以下是使用自动微分 (autograd) 的优势：

  • 灵活 - 在定义网络时提供的灵活性是使用 autograd 的巨大好处之一。我们可以在每次迭代中更改操作。这些被称为动态图，在需要静态图的框架中实现起来要复杂得多。即使在这种情况下，autograd 仍然能够正确地反向传播梯度。

  • 自动 - Autograd 是自动的，即反向传播过程的复杂性由它为您处理。我们只需要指定我们感兴趣计算哪些梯度。

  • 高效 - Autogard 高效地计算梯度。

  • 可以使用原生 Python 控制流运算符 - 我们可以使用原生的 Python 控制流运算符，例如 if 条件和 while 循环。autograd 仍然能够高效且正确地反向传播梯度。

在 MXNet Gluon 中使用 autograd

在这里，我们将通过一个示例了解如何在 MXNet Gluon 中使用autograd。

实现示例

在以下示例中，我们将实现一个具有两层的神经网络。实现后，我们将使用 autograd 自动计算损失相对于每个权重参数的梯度：

首先导入 autogrard 和其他所需的包，如下所示：

from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Loss

现在，我们需要定义网络，如下所示：

N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()

现在我们需要定义损失，如下所示：

loss_function = L2Loss()

接下来，我们需要创建虚拟数据，如下所示：

x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])

现在，我们准备进行第一次通过网络的前向传递。我们希望 autograd 记录计算图，以便我们可以计算梯度。为此，我们需要在autograd.record上下文中运行网络代码，如下所示：

with autograd.record():
   y_hat = N_net(x)
   loss = loss_function(y_hat, y)

现在，我们准备进行反向传递，我们通过对感兴趣的数量调用 backward 方法来启动它。在我们示例中，感兴趣的数量是损失，因为我们试图计算损失相对于参数的梯度：

loss.backward()

现在，我们有了网络中每个参数的梯度，优化器将使用这些梯度来更新参数值以提高性能。让我们检查第一层的梯度，如下所示：

N_net[0].weight.grad()

输出

输出如下：

[[-0.00470527 -0.00846948]
[-0.03640365 -0.06552657]
[ 0.00800354 0.01440637]]
<NDArray 3x2 @cpu(0)>

完整的实现示例

下面是完整的实现示例。

from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Loss
N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()
loss_function = L2Loss()
x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])
with autograd.record():
y_hat = N_net(x)
loss = loss_function(y_hat, y)
loss.backward()
N_net[0].weight.grad()
打印页面
上一页
下一页
广告