数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会科学
时尚研究
法律学C++ 中正 n 边正多边形的内切圆半径
n 边正多边形是 n 条边构成的闭合图形，这些边和角的长度全部相等。下图是一个 6 边正多边形，通常称为六边形。
内切圆半径是多边形中连接图形中心和边的线。它是垂直于其中一条边，因此长度最短。
接下来，我们推导它的长度公式。
一个 n 边多边形的边的夹角为360/n。
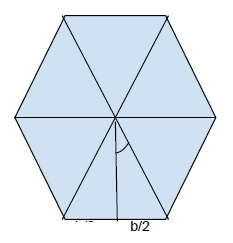
现在，如上图所示，角度等于 (360 / n )/2 = 180 /n
现在，以三角形为例，我们可以得出结论：
tan ø = b/2 / h = b/2h 2h * tan ø = b h = b/2*tanø , ø = 180 /n h = b/2*tan(180/n)
让我们用程序实现这一点，找出给定多边形的边数和每条边的长度时内切圆半径的长度。
公式
Given n = number of side , b = length of each side. h = length of apothem, h = b/2 * tan(180/n)
示例
#include<iostream>
#include <math.h>
using namespace std;
void apothemLength(int n, float a){
if (a < 0 && n < 0)
cout<<"invalid values";
else
cout<<"the length of apothem = "<< (a/(2*tan((180/n)*3.14159/180)));
}
int main(){
float a = 12;
int n = 9;
apothemLength(n, a);
return 0;
}输出
the length of apothem = 16.4849
更新于： 2019-10-24
203 次浏览
广告