数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++中已知边长的n边正多边形的面积
在本问题中，为了找到已知边长的n边正多边形的面积，我们将推导出该图形面积的公式，并基于此公式创建一个程序。但在那之前，让我们回顾一下基础知识，以便更容易理解主题。
n边正多边形是一个n边的多边形，其中所有边都相等。例如正五边形、正六边形等。
面积是任何二维图形范围的定量表示。
为了找到这个图形的面积，我们需要找到图形中各个三角形的面积，并将其乘以它拥有的边数。因为我们给出了n边。
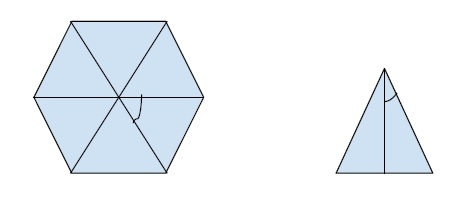
现在，从上图可以看出，我们可以为面积创建一个公式。
正多边形的每条边都可以构成一个边长为a（多边形的边长）且角度为180 / n（n是多边形的边数）的三角形。因此，可以使用以下公式求出面积：
三角形面积 = ½ * b * h
现在，h = a * tan(180/n)
So , area = ½ * a * a / 2 * tan(180/n) = a * a / (4 * tan(180/n))
使用此公式计算多边形的单个三角形的面积，我们可以计算整个多边形的面积：
n边正多边形的面积 = n * (a * a / (4 * tan(180 /n)))
算法
Step 1 : calculate the value of angle using (180 / n) Step 2 : Calculate the area of regular polygon using n * (a * a / (4 * tan(180 /n))) . Step 3 : Print the area of polygon.
示例
#include<iostream>
#include<math.h>
using namespace std;
int main(){
float a = 12, n = 9;
float area=(a * a * n) / (4 * tan((180 / n) * 3.14159 / 180));
cout<<"The area of "<<n<<" sided regular polygon of side "<<a<<" is "<<area;
return 0;
}输出
The area of 9 sided regular polygon of side 12 is 890.183
更新于：2019年10月16日
853 次浏览
广告