椭圆的面积

---

介绍

椭圆的面积是指椭圆在二维空间中所覆盖的区域或面积。椭圆看起来像一个规则的卵形，当圆锥体被斜面截断，且截面不与圆锥体的底面相交时，就会形成一个封闭的曲线，即椭圆。

椭圆是平面内到两个定点距离之和为常数的点的轨迹。这两个定点位于曲线内部，称为焦点（单数：焦点）。这个常数的比值称为椭圆的离心率，用字母'e'表示。这个定线称为准线。

在我们的日常生活中，可以找到许多椭圆形的物体，例如板球场、羽毛球拍、行星轨道等等。在本教程中，我们将讨论椭圆的面积。

椭圆

椭圆是圆锥曲线的一部分，具有与圆相似的特征。与圆不同，椭圆具有卵形。椭圆的离心率小于1，表示到椭圆两个焦点距离之和为常数的点的轨迹。

椭圆的特征

• 有几个特征可以帮助我们从其他类似的形状中识别出椭圆。这些椭圆的属性如下：

• 当平面与圆锥体以其底角相交时，就会形成椭圆。

• 每个椭圆都有两个焦点或焦距。椭圆上任意两点到两个焦点的距离之和为常数。

• 所有椭圆都有一个中心，以及一个长轴和一个短轴。

• 所有椭圆的离心率都小于1。

椭圆的面积

椭圆的面积是指椭圆所覆盖的二维面积或区域。椭圆是一个二维图形，由连接平面上所有到两个定点距离之和为常数的点形成。这两个定点称为椭圆的焦点。

椭圆的长轴是椭圆中最长的弦。垂直平分长轴的弦称为短轴。

如果已知长轴和短轴的长度，则可以使用通用公式计算椭圆的面积。计算椭圆面积的公式如下：

$$\mathrm{椭圆面积 = π a b}$$

a = 半长轴长度

b = 半短轴长度

椭圆的通径长度

通径是一条穿过椭圆焦点的直线，并且垂直于水平轴。由于椭圆有两个焦点，因此它有两个通径。

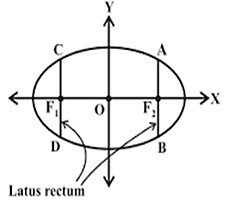
这是一个椭圆的图形，其方程为

$$\mathrm{\frac{x^2}{a^2} +\frac{y^2}{b^2} =1}$$

其中 2a 是长轴的长度，2b 是短轴的长度。

CD 和 AB 是椭圆的通径，点 A 的坐标为 $\mathrm{(ae,\frac{b^2}{a})}$，点 B 的坐标为 $\mathrm{(ae,-\frac{b^2}{a})}$，点 C 的坐标为 $\mathrm{(-ae,\frac{b^2}{a})}$，点 D 的坐标为 $\mathrm{(-ae,-\frac{b^2}{a})}$，其中 e 是椭圆的离心率。

因此，椭圆的通径长度为

$$\mathrm{|\frac{b^2}{a}|+|\frac{b^2}{a}|=\frac{2b^2}{a}}$$

注意

• 平面内到两个定点距离之和为常数的点的轨迹是椭圆。

• 椭圆面积 = π a b

• 将 π 的值视为 3.14 或 22/7

• 确定半长轴 (a) 和半短轴 (b) 的值，然后应用椭圆面积公式。

例题

1) 求长轴和短轴长度分别为 2 和 4 的椭圆的面积。

解答：我们知道，如果给出短轴和长轴的长度，则计算椭圆面积的公式为椭圆面积 = π a b。

$$\mathrm{椭圆面积 = π a b}$$

$$\mathrm{椭圆面积 = π ×2×4}$$

$$\mathrm{椭圆面积 = 8π }$$

2) 求长轴和短轴长度分别为 8 和 3 的椭圆的面积。

解答：我们知道，如果给出短轴和长轴的长度，则计算椭圆面积的公式为椭圆面积 = π a b。

$$\mathrm{椭圆面积 = π a b}$$

$$\mathrm{椭圆面积 = π ×8×3}$$

$$\mathrm{椭圆面积 = 24π }$$

3) 如果椭圆的方程为 $\mathrm{\frac{x^2}{16}+\frac{y^2}{144}=1}$，则求通径的长度。

解答：已知椭圆的方程为 $\mathrm{\frac{x^2}{16}+\frac{y^2}{144}=1}$

$$\mathrm{\Rightarrow \frac{x^2}{4^2}+\frac{y^2}{12^2}=1}$$

现在将此方程与 $\mathrm{\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 进行比较

$$\mathrm{\Rightarrow a=4 and b=12}$$

我们知道通径的长度为 $\mathrm{\frac{2b^2}{a}}$

因此，通径的长度 = $\mathrm{\frac{2(12)^2}{4}=72}$

4) 如果椭圆的方程为 $\mathrm{\frac{x^2}{16}+\frac{y^2}{121}=1}$，则求通径的长度。

解答：给定的方程为 $\mathrm{\frac{x^2}{16}+\frac{y^2}{121}=1}$

$$\mathrm{\Rightarrow \frac{x^2}{4^2} +\frac{y^2}{11^2} =1}$$

现在将此方程与 $\mathrm{\frac{x^2}{a^2}+\frac{y^2}{11^2}=1}$ 进行比较

$$\mathrm{\Rightarrow a=4\: and\: b=11}$$

我们知道通径的长度 = $\mathrm{\frac{2b^2}{a}}$

因此，椭圆的通径长度 $\mathrm{\frac{2(11)^2}{4}=\frac{121}{2}}$

5) 给定椭圆 $\mathrm{\frac{x^2}{16}+\frac{y^2}{25}=1}$ 的面积是多少？

解答：已知椭圆的方程为 $\mathrm{\frac{x^2}{16}+\frac{y^2}{25}=1}$

$$\mathrm{\Rightarrow \frac{x^2}{4^2}+\frac{y^2}{5^2}=1}$$

现在将此方程与 $\mathrm{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 进行比较

$$\mathrm{\Rightarrow a=4\: and\: b=5}$$

现在应用公式

$$\mathrm{椭圆面积 = π a b}$$

$$\mathrm{椭圆面积 = π ×4×5}$$

$$\mathrm{椭圆面积 = 20π }$$

结论

椭圆内部存在的区域数量定义为其面积。或者，椭圆的面积是可以放入其中的单位正方形的总数。

椭圆的面积是 π 与半长轴和半短轴长度的乘积。

常见问题

1. 椭圆的面积是什么意思？

椭圆内部存在的区域数量定义为其面积。

2. 椭圆的通径长度是多少？

椭圆的通径长度为 $\mathrm{\frac{2b^2}{a}}$。

3. 通径是什么意思？

通径是一条穿过圆锥曲线焦点的直线

并且平行于圆锥曲线的准线方向。

4. 什么是椭圆？

与圆不同，椭圆具有卵形。椭圆的离心率小于1，表示到椭圆两个焦点距离之和为常数的点的轨迹。

5. 椭圆面积的公式是什么？

计算椭圆面积的公式如下：

$$\mathrm{椭圆面积 = π a b}$$

a = 半长轴长度

b = 半短轴长度