伯努利原理

---

简介

伯努利原理可以用简单的解释来理解：当流体从大直径管道流向小直径管道时，流体的速度会大大增加。是的，这是真的，但就这么简单吗？一点也不。这个原理相当复杂，许多公式和因素控制着它。全世界有许多应用利用了这个美丽的原理。解释伯努利原理的一个常见例子是，当火车经过站台时，如果你站在站台边上，你会感觉到被火车吸过去，这就是由于这个原理。运动的火车在其附近造成低压。这种低压将附近的物体拉向它。让我们在这篇文章中详细了解伯努利原理。

什么是伯努利原理？

该原理指出，在流线型流体流动中，沿流线的各种能量之和是相同的且恒定的。这三种能量是动能、势能和施加于流体的外部压力。假设管道在某一点从地面升起，那么由于高度差，管道的这一部分会增加更多的势能。当管道在流线型中直径减小时，流体速度会增加，结果动能会增加。

伯努利原理公式

这个概念的公式或多或少与能量守恒定律有关。流线型流体流动在任何时间和管道位置的总能量都是相等的。正如您参考下图所示，管道的中心部分较窄，您可以观察到该部分流体的速度以及动能更大。因此，这里有一些可以辨别的推论。

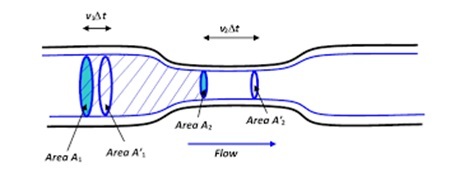
当管道直径减小时，横截面积减小，流速和压力增加，流量减小。

$$\mathrm{P+\frac{1}{2}\rho v^2+\rho gh=constant}$$

伯努利方程的推导

处理该方程时需要记住的两个标准是：流体不应具有粘性，并且流体流动应为层流。参考下图，我们将推导出伯努利方程。

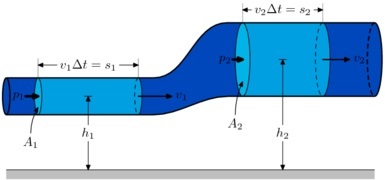
anonymous, BernoullisLawDerivationDiagram, CC BY-SA 3.0

为了使流体流动发生，我们知道会做外部功，并且这项功与其他功（如重力）协商后，会导致沿流体路径的压力差。因此，所做的功由下式给出

$$\mathrm{W=F_1 dx_1-F_2 dx_2}$$

$\mathrm{dx_1=}$ 窄管长度

$\mathrm{dx_2=}$ 宽管长度

压力等于单位面积上的力。

即 $\mathrm{P=\frac{F}{A}}$

所以

$$\mathrm{F=P×A}$$

将力代入上述方程，

$$\mathrm{dW=P_1 A_1 dx_1-P_2 A_2 dx_2}$$

$$\mathrm{dW=P_1 dV-P_2 dV=(P_1-P_2 )dV }$$

$$\mathrm{dV=Adx}$$

动能的变化表示如下。

$$\mathrm{dK=\frac{1}{2}m_1v_1^2-\frac{1}{2}m_2v_2^2}$$

注意，m是流体一部分的质量，v是速度。

由于 $\mathrm{mass = density\:\times \:volume}$

$$\mathrm{dK=\frac{1}{2}\rho dV(v_2^2-v_1^2)}$$

现在找到势能的变化，

$$\mathrm{ dU=mgh_2-mgh_1=ρdVg(h_2-h_1)\:\:\:\:dW=dK+dU}$$

$$\mathrm{(P_1-P_2)dV=\frac{1}{2}\rho dV(v_2^2-v_1^2)}$$

在两边消去dV，我们得到

$$\mathrm{(P_1-P_2)=\frac{1}{2}\rho (v_2^2-v_1^2 )+\rho g(h_2-h_1)}$$

重新排列上述方程，我们得到如下所示的伯努利方程。

$$\mathrm{P_1+\frac{1}{2}\rho v_1^2+\rho gh_1=P_2+ \frac{1}{2} \rho v_2^2+\rho gh_2}$$

连续性原理

管道横截面积与流体在任何点的速度的乘积始终是一个常数。这就是连续性原理。如果$\mathrm{A_1}$和$\mathrm{A_2}$是两端的横截面积，$\mathrm{V_1}$和$\mathrm{V_2}$是流体在相应端的流速，那么我们可以写成：

$$\mathrm{A_1 V_1 = A_2 V_2}$$

伯努利原理的应用

该原理的基本原理被应用于飞机空气动力学的设计要素中，用于流体动力学的专家研究和实验，以及渡轮的设计研究（两艘船并排系在一起）等。

能量守恒与伯努利方程之间的关系

该方程说明了在层流流体流动中，当流速增加时，压力降低的原理。因此，对于非粘性流体，能量守恒在运动能量、静态能量和压力能量之间以相互的方式发生。

恒定深度下的伯努利方程

当考虑“恒定深度”的情况时，这是考虑方程变化的一种独特方式。在这种情况下，我们需要使两个高度h1和h2相等。即h1=h2。然后方程简化为：

$$\mathrm{P_1+\frac{1}{2}\rho v_1^2=P_1+\frac{1}{2}\rho v_2^2}$$

静态流体的伯努利方程

该方程可应用于静态流体，其中流体不流动。它是静态的。这意味着，我们可以对方程中的$\mathrm{v_1}$和$\mathrm{v_2}$赋予0值。然后方程简化为：

$$\mathrm{P_1+\rho gh_1=P_2+\rho gh_2}$$

伯努利原理示例

每当物体发生偏离，无论是出于良好目的还是作为自然反应，并且这是由于空气或非粘性流体的运动造成的，那么那里就包含了伯努利原理。

• 飞机升力是由于螺旋桨在机翼下产生的高压空气产生低压，从而将飞机抬升。

• 当龙卷风袭击固定屋顶时，由于龙卷风在屋顶上方的速度，压力降低，屋顶就会飞走。

• 板球的旋转是由于投球手投球的特定方式，以及投球手将球的一个半球抛光得非常光亮，而保持球的另一个半球粗糙的原因。

• 快速行驶的火车会因其极高的速度在其路径上产生一段时间内的低压区域而产生拉力。烟囱、喷雾器等等，你有很多日常生活中伯努利原理的例子。

结论

伯努利原理适用于平稳流动的流体。当流体流过具有两个横截面积的管道时，较小直径的管道会为流体创造更大的速度和压力，而流量会减小。这种现象可以在日常生活中许多情况下观察到。由于该原理来自能量守恒原理，并定义了一个方程来描述其作用，因此该原理被应用于许多关键应用设计中，例如飞机的空气动力学。

常见问题

Q1. 流体的水平流动与伯努利原理有何关系？

A1. 水平流动可以视为恒定深度。您必须在方程中取$\mathrm{h_1=h_2}$。

Q2. 什么是夹带装置？

A2. 夹带装置是使用外力使高压流体流动的装置，然后将一种流体夹带到另一种流体中。例如，车辆的喷雾器、喷漆器和化油器。

Q3. 伯努利方程中应用了哪三个水头？

A3. 速度水头、压力水头和高度水头。

Q4. 能量守恒定律是什么，伯努利原理是从哪里推导出来的？

A4. 能量守恒定律指出作用于物体的所有能量的总和是恒定的原理。当物体的势能（随着高度增加）增加时，其相关的动能将减小，以使总和保持恒定。能量守恒定律的方程是

$$\mathrm{\frac{1}{2}mv^2+mgh=constant}$$

Q5. 文丘里效应是什么？

A5. 它是一种狭窄的管道，由于产生的低压，用于增加流体的速度。文丘里效应是我们在一直讨论的原理的另一个名称。