数学归纳法的原理

---

简介

数学归纳法涉及一些原理，这些原理是一种特殊的技巧，用于证明代数中以 n 表示的定理和陈述；其中 n 属于自然数。在数学归纳法中，任何陈述都首先证明 n=1 的情况，然后证明对于任何变量都成立。

什么是 PMI？

数学归纳法可以描述为一种工具，用于证明任何陈述 A(n)，该陈述对于自然数 n=1、2、3、4、5......n 都成立。数学归纳法基于一些称为数学归纳法原理 (PMI) 的原理。

为了证明关于陈述 A(n) 的结果，我们可以使用数学归纳法的原理。首先，我们检查该陈述是否对 A(1) 成立。然后，如果该陈述对 A(1) 成立，我们假设它也对 A(x) 成立，其中 x 表示直到 x 的所有数字，并将相同的假设应用于 A(x+1) 也成立。如果 A(x+1) 成立，则陈述 A(x) 对所有自然数都成立。

数学归纳法的第一个原理

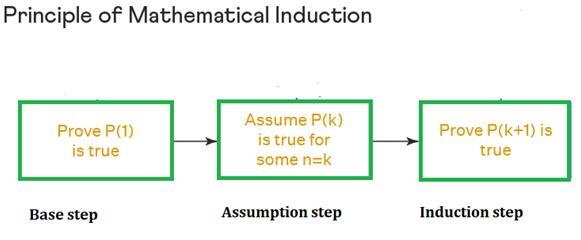
让我们深入了解数学归纳法的第一个原理，并学习用于证明该陈述的步骤。

假设有一个陈述 A(n)，其中 n 属于自然数。

现在让我们证明如果该陈述对 n = 1 成立，即如果 A(1) 成立与否。

如果该陈述对 n=1 成立，那么我们检查该陈述对 n = x 是否成立，其中 x 是一个自然数。

如果该陈述对 n =x 成立，那么该等式对 $\mathrm{P(x\:+\:1)}$ 也成立。因此，可以确定陈述 A(n) 对 $\mathrm{n\:\varepsilon\:N}$ 成立。

例题解析

现在让我们看一个基于第一个 PMI 的例子。

让我们假设一个陈述 $\mathrm{n\:\varepsilon\:N}$

$$\mathrm{1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:n^{2}}$$

答案 −

令给定陈述 A(n) 定义为 $\mathrm{A(n)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:n^{2}}$ ，其中 $\mathrm{n\:\varepsilon\:N}$

基础步骤 - 注意 A(1) 成立

因为通过将 n=1 代入，我们得到

$\mathrm{1\:=\:1^{2}}$

假设步骤 - 假设 A(x) 对某个 $\mathrm{x\:\varepsilon\:N}$ 成立，

即，$\mathrm{A(x)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:x^{2}}$

归纳步骤 - 为了证明 P(x + 1) 成立，

$\mathrm{A(x)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:+\:(2n\:+\:1)\:=\:x^{2}\:+\:(2x\:+\:1)}$

$$\mathrm{=\:x^{2}\:+\:2x\:+\:1\:=\:(x\:+\:1)^{2}}$$

因此，当 $\mathrm{x\:\varepsilon\:N}$ 时，A(x + 1) 成立。因此，A(x) 对某个 $\mathrm{x\:\varepsilon\:N}$ 成立

因此，根据 PMI，A(n) 对所有自然数都成立。

数学归纳法的第二个原理

现在我们已经了解了第一个 PMI，让我们了解一下第二个 PMI 是什么以及它可以在哪里使用。假设我们有一个数学表达式 A(n)，它对所有 n ∈ N 都成立。我们知道证明的步骤是，如果该表达式对 A(1) 成立，然后对任何数字 x 成立，那么它必须对 P(x+1) 成立。当我们尝试在考虑复合数后证明它时，问题就出现了。例如，如果我们假设 A(29) 是一个成立的表达式，并且我们必须使用它来证明 P(30) 也成立。如果我们将 30 因式分解为 30 = 2 × 15，则 A(29) 成立的表达式不能用于证明 A(30) 也成立。

因此，我们需要第二个原理来证明归纳法。我们假设一个表达式成立，并用它来证明它对下一个数字也成立。第二个原理背后的逻辑是我们假设该表达式对所有先前的表达式都成立，并用它来证明下一个表达式也成立。在第二个原理中，我们根据自然数的子集陈述该陈述。在许多情况下，我们将使用 I=1 或 I=0。

令 I 为任何整数，S 是 Y 的一个子集，使得

• $\mathrm{I\:\varepsilon\:N}$

• 对于每个 $\mathrm{x\:\varepsilon\:Y}$，其中 $\mathrm{x\:\varepsilon\:Y}$，如果 $\mathrm{\lbrace\:n\:\varepsilon\:Y\:|\:n\:\geq\:I\:\rbrace\:\subseteq\:S}$

例题解析

1) 对于一个数学陈述 $\mathrm{n\:=\:3a\:+\:5b}$，找出存在哪些自然数 (n) 使得整数 a 和 b 为非负整数？

答案 −

令陈述 A(n) 对 $\mathrm{n\:=\:3a\:+\:5b}$ 成立，其中 $\mathrm{a\:\geq\:0\:or\:b\:\geq\:0}$

让我们看看该陈述是否对 a=0 和 b=0 成立。

$$\mathrm{n\:=\:3\:\times\:0\:+\:5\:\times\:0\:=\:0}$$

所以它不成立。

现在例如，如果 $\mathrm{a\:>\:0}$，即 $\mathrm{a\:=\:1\:,\:b\:=\:0}$

那么 $\mathrm{3\times\:1\:+\:5\times\:0\:=\:3}$

如果 $\mathrm{b\:>\:0}$，即，$\mathrm{b\:=\:1\:,\:a\:=\:0}$

那么 $\mathrm{3\times\:0\:+\:5\times\:1\:=\:5}$

因此，我们可以说，如果 a>0 或 b>0，则 $\mathrm{3a\:+\:5b\:\geq\:3}$

但我们看到 A(7) 不成立。

如果我们必须证明 A(8) 是否成立，我们不能使用 A(7) 来证明它。

A(8) 对 a=1 和 b=1 成立，因为 $\mathrm{3\times\:1\:+\:5\times\:1\:=\:8}$

因此，我们可以说，对于每个 $\mathrm{n\:\varepsilon\:N\:with\:n\:\geq\:8}$，都存在非负整数 a 和 b，使得

$$\mathrm{n\:=\:3a\:+\:5b.}$$

结论

数学归纳法是证明一个数学陈述对于所有自然数 n 是否成立的概念。数学归纳法以原理的形式进行推广。数学归纳法涉及一些原理，这些原理是一种特殊的技巧，用于证明代数中以 n 表示的定理和陈述；其中 n 属于自然数。在数学归纳法中，任何陈述都首先证明 n=1 的情况，然后证明对于任何变量都成立。为了证明一个陈述，有两个原理

基础步骤 - 在此步骤中，我们证明 A(1) 是否成立。

假设步骤 - 在第二步中，我们假设 A(x) 对自然数 x 成立。归纳步骤：在最后一步中，我们证明 $$\mathrm{A(x\:+\:1)} 是否成立。

如果所有步骤都成立，那么我们可以说“使用 PMI，P(n) 对所有自然数都成立”。

常见问题

1. 第一个 PMI 中的步骤名称是什么？

第一个 PMI 中涉及的步骤是基础步骤、假设步骤和归纳步骤

2. 矩阵中的 PMI 是什么？

在矩阵中，PMI 是基于矩阵证明陈述的概念。

3. 什么是数学归纳法？

一个利用基于既定原理的步骤来证明数学陈述的过程。

4. 数学归纳法中的归纳假设是什么？

PMI 中的第二步，即假设步骤，称为归纳假设

5. 弱归纳法和强归纳法有什么区别？

在弱归纳法中，我们假设任何在 A(x) 步骤中为真的陈述，而在强归纳法中，给定的陈述 A(n) 从基础到 A(x) 步骤的所有步骤都为真。