阿基米德原理解释

---

介绍

阿基米德原理是流体力学中的一个重要原理。它是由希腊数学家和科学家阿基米德发现的。该原理用于估算形状不规则的物体的体积、物体的密度和物体的比重。

什么是阿基米德原理？

放置在流体（液体或气体）中的物体将受到向上的浮力。该力等于物体排开的流体量。对于完全浸没或部分浸没的物体，物体排开的流体体积将等于该物体的体积。

阿基米德原理的陈述

如果一个物体全部或部分浸入静止的液体中，其重量的一部分似乎消失了。物体这种表观重量的损失等于物体排开的液体的重量。

阿基米德原理公式

阿基米德流体定律指出，由于流体作用在物体上的浮力等于物体排开的流体的重量。阿基米德定律的数学表达式可以写成：

$$\mathrm{F=\rho Vg}$$

这里，

F=作用在浸没物体上的浮力

ρ=流体的密度

V=排开流体的体积

阿基米德原理推导

让我们考虑一个浸在密度为ρ的液体中的立方体。立方体ABCD和EFGH表面距液体上表面的深度分别为$\mathrm{h_2}$和$\mathrm{h_1}$。立方体各边的长度为l。液体在立方体的每个表面上都施加一个法向推力。作用在立方体相互相对的垂直面ABHE和CDFG上的横向推力相等且方向相反。

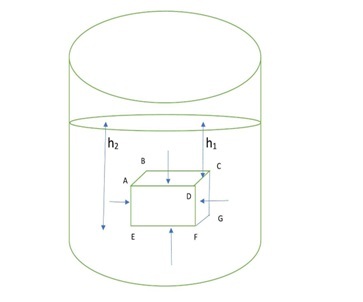
同样，作用在面AEFD和BCGH上的横向推力相互平衡。因此，在水平方向上，合横向力为零。但是，由于这些表面距液体上侧的深度不同，因此在表面ABCD和EFGH上会产生不相等的推力。

ABCD上任意一点的液体向下压力为$\mathrm{\rho gh_1}$

ABCD上的向下推力为$\mathrm{l^2\:\rho gh_1}$

EFGH上任意一点的液体向上压力为$\mathrm{\rho\:gh_2}$

然后，EFGH上的向上推力为$\mathrm{l^2 \rho gh_2}$

由于$\mathrm{h_2 > h_1}$，作用在立方体上的向上推力大于向下推力。

然后，

净向上推力$\mathrm{l^2\:\rho gh_2-l^2 ρgh_1=l^2 \rho g(h_2-h_1)=l^3 \rho g }$

由于，$\mathrm{h_2-h_1=l }$

但是，$\mathrm{l^3=V (立方体的体积)}$

因此，

$$\mathrm{F = l^3\:\rho\:g=V\:\rho g}$$

因此，立方体上的浮力=立方体排开的液体的重量。

漂浮定律

有三个漂浮定律。因此，设W为物体的重量，w为浮力。

• 如果W>w，即物体的重量大于浮力，则物体将沉到底部。

• 如果W<w，即物体的重量小于浮力，则物体将部分浸没在液体中漂浮。

• 如果W=w，即物体的重量等于浮力，则如果物体的整个体积刚好浸没在液体中，则物体将漂浮在液体中。

阿基米德原理示例

示例 1：一块体积为 20.5 cm3 的木头系在一块体积为 1 cm³ 的铅块上。说明该组合体在水中是漂浮还是下沉。[木材和铅的比重分别为 0.5 和 11.4]。

答：$\mathrm{铅的重量=(1×11.4)gm×g=11.4gm×g}$

$\mathrm{木块的重量\: =(20.5×0.5)gm×g=10.25gm×g}$

$$\mathrm{总重量=21.65\:gm×g}$$

$\mathrm{总体积=(20.5+1)cm^3=21.5Cm^3}$

因此，组合体排开水的重量=21.5gm×g

因此，组合体的重量>排开水的重量

因此，该组合体将沉入水中。

阿基米德原理实验

根据阿基米德原理，

$$\mathrm{表观重量=物体的重量-浮力 }$$

让我们看一个实验，

• 让我们取一个装满水的容器。该容器与一个碗连接，以便如果水溢出，它将通过管道将碗排空。

• 现在取任何固体物体，并使用弹簧秤在空气中测量其重量。记下该值，为 6 公斤。

• 接下来，将物体连接到弹簧秤上并将其浸入水中。弹簧秤必须在水面以上。

• 现在，当重量降低时，一些水将进入碗中。排开水的重量为 2 公斤。

• 弹簧秤将显示的值小于之前的值。记下该值，为 4 公斤。

• 我们发现，当我们将物体的新的重量从第一次测量的值中减去时，它将等于排开水的重量。

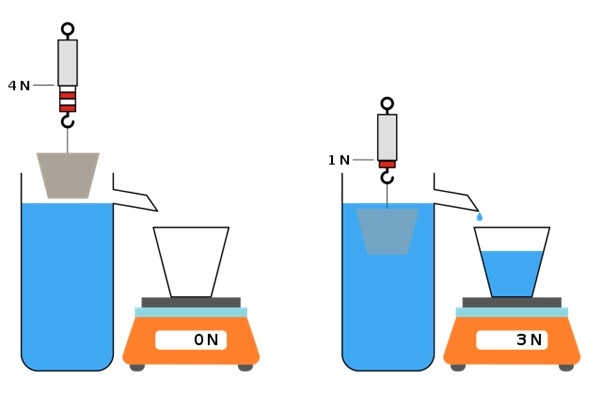
MikeRun，阿基米德原理，CC BY-SA 4.0

阿基米德原理的应用

气球的向上运动

气球的向上运动取决于空气的推力。气球的净重量与它排开的空气相比要小得多。因此，作用在气球上的浮力大于其重量。因此，气球受到向上的合力并向上移动。

潜艇

潜艇可以潜入水中，也可以漂浮在水面上。潜艇由配重舱组成，这些舱可以装满空气或水。当这些舱装满空气时，潜艇漂浮在水上，因为潜艇的重量低于它排开的水的重量。当水被允许进入这些舱时，潜艇的重量变得大于它排开的水的重量，因此潜艇下沉。

救生衣

救生衣是一个充气的袋子。救生衣和人的重量小于排开水的重量。因此，通过穿救生衣，人可以漂浮。

结论

部分或完全浸入液体中的物体将经历重量损失。这种重量损失相当于物体排开的液体的重量。这被称为阿基米德原理。此规则不适用于处于失重状态的物体，例如人造卫星或自由落体。阿基米德原理适用于潜艇、救生衣、气球、游泳、船舶等。借助该原理，可以确定任何形状的固体的体积、物质的密度等。

常见问题

Q1. 什么是浮力？

答：流体在静止状态下对浸在其中的物体施加向上力的能力称为浮力。

Q2. 解释阿基米德原理是否适用于重力作用下的自由落体。

答：我们知道，自由落体是失重的。因此，在这种情况下，该原理不适用。因为自由落体是失重的。

Q3. 鸡蛋在淡水中下沉，但在盐水中漂浮。为什么？

答：鸡蛋的密度高于淡水。因此，它会沉入水中。但是，当向水中加入适量的盐时，盐水的密度会高于鸡蛋，鸡蛋就会漂浮在盐水上。

Q4. 阿基米德原理是否适用于围绕太阳运行的人造卫星内部？

答：围绕太阳运行的人造卫星内部所有物体都处于失重状态。因此，物体和物体排开的流体的重量都将为零，并且物体不会受到任何浮力。因此，阿基米德原理不适用于围绕太阳运行的人造卫星内部。

Q5. 一个实心球和一个空心球，具有相同的质量和外半径，浸没在相同的液体中。哪个会感觉更重？

Ans. 实心球和空心球的半径和体积都相等。因此，它们排开的液体体积相同。所以，两种情况下重量的损失都相等，两个球的视重也相同。