箱线图

---

介绍

箱线图可以用于显示和分析数据。有时需要更详细地了解各种分布或数据集中的信息，而平均数、中位数和众数等集中趋势的度量可能无法满足要求。数据的变异性或离散性需要一个更具体的依据。箱线图可以满足这一需求。

箱线图是一种使用区间尺度估计数据集的方法。它也被称为盒形图。这些主要用于解释数据。它是一种图形方法，显示数据集内数据的变化。

在本教程中，我们将讨论箱线图。

定义

• 箱线图是一种图表，它使我们能够更清楚地了解数据中的值应该如何分布。箱线图从箱体延伸出线条，这些线条通常被称为须线。

• 须线用于表示上四分位数和下四分位数之外的变化。箱线图的一个特点是它是非参数的。而箱线图的这一特性实际上有助于在样本中显示统计总体变化，在这些样本中没有对潜在的统计分布做出任何假设。

• 箱体中的间隙表示数据中的离散程度（扩展）和偏度，以及异常值的存在。

• 箱线图可以水平或垂直绘制。箱线图是探索性数据分析中常用的图表。

如何绘制

箱线图可以通过五个简单的步骤绘制。要创建箱线图，我们必须首先确定 -

• 步骤 1 - 最小值是数据中最小的值。

• 步骤 2 - 第一四分位数定义为小于数据集中较低 25% 的值。

• 步骤 3 - 从提供的数据集中确定中位数。

• 步骤 4 - 第三四分位数的值大于较低 25% 的值。

• 步骤 5 - 最大值是给定数据集的最大值。

类型

箱线图（或箱形图）是一种简单的方法，用于绘制数据在四分位数上的分布。这是一种基于最低、第一、中间、第三和最高值的统计数据的图形表示。

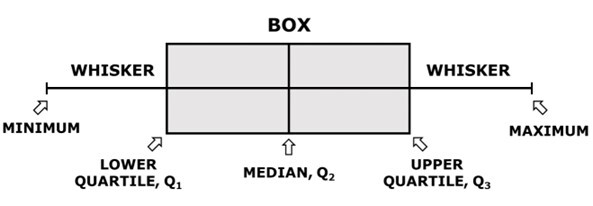
让我们检查这五个箱线图组件。

中位数

按升序或降序排列的一系列值中间的值或数量。如果集合有奇数个值，则中位数位于正中间。如果值的个数为偶数，则中位数是通过计算最接近中心的两个值的平均值来计算的。

下四分位数

下四分位数（也称为第一四分位数）将数据分成底部 25%。四分位数是三个数据点，将信息记录分成四个相等的部分。每个部分代表整个数据集的四分之一。下四分位数是中间下半部分的值。

上四分位数

上四分位数的另一个名称是第三四分位数。将数据分成底部 75%（或顶部 25%）。它也是上半部分的平均值。

四分位距

表示下四分位数和上四分位数之间的差值。IQR 通常被认为比范围更好的离散度量，因为它不受异常值（最高-最低）的影响。

最高值

此箱线图点表示生成箱线图的数据分布中最高的非异常值。与数据集的最大值不匹配。

最低值

此箱线图点不是异常值，因为它表示用于创建箱线图的数据分布（分布的最小四分位距）的最小值。不再与数据集的最小值匹配。

已解决示例

1) 假设一家电脑公司有两个地点。每个月，公司都会跟踪每个商店的销售数量。我们在过去 12 个月中售出了以下数量的电脑。

第一家店 − 350、460、20、160、580、250、210、120、200、510、290、380。

第二家店 − 520、180、260、380、80、500、630、420、210、70、440、140。

答案 - 创建两个箱线图，一个用于商店 1，一个用于商店 2，以比较两家商店的销售业绩。

首先，按升序排列数据点。

20, 120 , 160 , 200, 210, 290 , 350 , 380 , 460 , 510, 580.

现在我们必须计算中位数。另一方面，这是一个平衡的数据集。中间没有单个点。在我们的例子中，第六个和第七个数据点 250 和 290 表示中间。

在偶数数据集里，中位数计算如下 -

$$\mathrm{Median\:=\:\frac{250\:+\:290}{2}\:=\:270}$$

考虑一下在偶数数据集中使用下四分位数和上四分位数时会发生什么：六个数小于中位数 - 20、120、160、200、210 和 250。

这六个项目的平均值是下四分位数，所以 $\mathrm{=\:\frac{(160\:+\:200)}{2}\:=\:180}$

还有六个数大于中位数 - 290、350、380、460、510、580。

这六个数据点的平均值是上四分位数=420

最后，商店 1 的销售额由五个数字概括 - 20、180、270、420 和 580。

商店 2 的五数概括是使用相同的计算得出的。70、160、320、470 和 630

我们几乎完成了比较箱线图 -

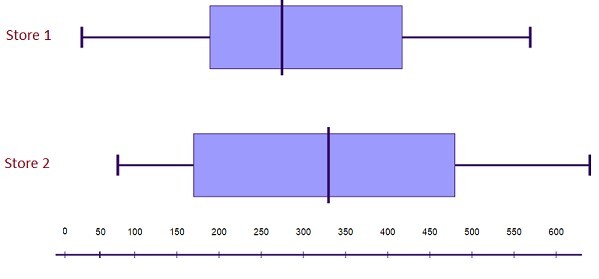
结果：商店 2 的四分位距更大。这些结果表明商店 2 的销售额始终高于商店 1。

结论

在本教程中，我们学习了箱线图、它们的属性和重要性。箱线图可以用于显示和分析数据。它们包含许多必须进一步研究的关键参数。此外。可以在同一图表中表示多个数据集。

常见问题解答

1. 箱线图是什么意思？

箱线图是一种图表，它提供给定数据集的五个数字的概述。最小值、下四分位数、中位数、上四分位数和最大值

2. 箱线图的五数概括是什么？

箱线图的五数概括是最小值、最大值、中位数、第一四分位数和第三四分位数。

3. 什么时候说箱线图是对称的？

如果中位数到最小值和最大值的距离相等，则称箱线图是对称的。

4. 使用箱线图的缺点是什么？

箱线图的缺点是隐藏了多峰性和其他分布特征。平均值难以定位，可能会让查看者感到困惑。

5. 箱线图中的异常值到底是什么？

异常值是在数值上与数据集中其余数据不同的数据点，并且位于箱线图之外。