数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中检查给定的二叉树是否为堆
概念
对于给定的二叉树，我们需要验证它是否具有堆属性。二叉树需要满足以下两个条件才能成为堆：
二叉树应该是一棵完全二叉树（即除了最后一层外，所有层都应该填满）。
二叉树的每个节点的值都应该大于或等于其子节点（考虑最大堆）。
示例
对于以下示例，这棵树包含堆属性：
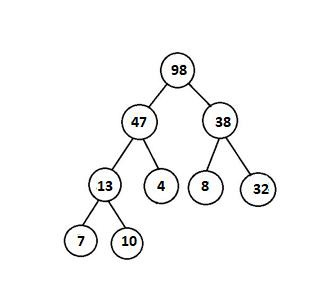
以下示例不具有堆属性：
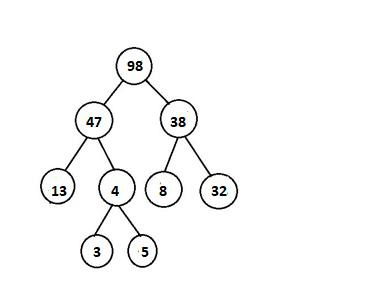
方法
需要分别验证上述每个条件，为了验证完整性，编写了 isComplete（此函数检查二叉树是否完整）和为了验证堆属性编写了 isHeapUtil 函数。
在编写 isHeapUtil 函数时，我们考虑以下几点：
每个节点最多可以有 2 个子节点，0 个子节点（最后一层节点）或 1 个子节点（最多只能有一个这样的节点）。
如果发现节点没有子节点，则它是一个叶节点并返回 true（基本情况）。
如果发现节点只有一个子节点（它必须是左子节点，因为它是一棵完全二叉树），则我们只需要将此节点与其唯一的子节点进行比较。
如果发现节点有两个子节点，则在节点处验证堆属性并在两个子树上递归。
示例
/* C++ program to checks if a binary tree is max heap or not */
#include <bits/stdc++.h>
using namespace std;
struct Node1{
int key;
struct Node1 *left;
struct Node1 *right;
};
struct Node1 *newNode(int k){
struct Node1 *node1 = new Node1;
node1->key = k;
node1->right = node1->left = NULL;
return node1;
}
unsigned int countNodes(struct Node1* root1){
if (root1 == NULL)
return (0);
return (1 + countNodes(root1->left) + countNodes(root1->right));
}
bool isCompleteUtil (struct Node1* root1, unsigned int index1, unsigned int number_nodes){
if (root1 == NULL)
return (true);
if (index1 >= number_nodes)
return (false);
// Recur for left and right subtrees
return (isCompleteUtil(root1->left, 2*index1 + 1, number_nodes) && isCompleteUtil(root1->right, 2*index1 + 2, number_nodes));
}
bool isHeapUtil(struct Node1* root1){
if (root1->left == NULL && root1->right == NULL)
return (true);
if (root1->right == NULL){
return (root1->key >= root1->left->key);
}
else{
if (root1->key >= root1->left->key &&
root1->key >= root1->right->key)
return ((isHeapUtil(root1->left)) &&
(isHeapUtil(root1->right)));
else
return (false);
}
}
bool isHeap(struct Node1* root1){
unsigned int node_count = countNodes(root1);
unsigned int index1 = 0;
if (isCompleteUtil(root1, index1, node_count) &&
isHeapUtil(root1))
return true;
return false;
}
// Driver program
int main(){
struct Node1* root1 = NULL;
root1 = newNode(10);
root1->left = newNode(9);
root1->right = newNode(8);
root1->left->left = newNode(7);
root1->left->right = newNode(6);
root1->right->left = newNode(5);
root1->right->right = newNode(4);
root1->left->left->left = newNode(3);
root1->left->left->right = newNode(2);
root1->left->right->left = newNode(1);
if (isHeap(root1))
cout << "Given binary tree is a Heap\n";
else
cout << "Given binary tree is not a Heap\n";
return 0;
}输出
Given binary tree is a Heap
更新于： 2020-07-23
294 次查看
广告