回路秩

设 G 为一个具有 n 个顶点和 m 条边的连通图。G 的生成树 T 包含 (n-1) 条边。

因此，为了得到生成树，你需要从 G 中删除的边的数量 = m-(n-1)，这称为 G 的回路秩。

这个公式是正确的，因为在生成树中你需要有 'n-1' 条边。在 m 条边中，你需要在图中保留 'n–1' 条边。

因此，从 m 中删除 'n–1' 条边得到需要从图中删除的边，以获得不形成环的生成树。

示例

查看以下图形 -

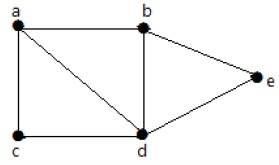
对于上面示例中给出的图，你有 m=7 条边和 n=5 个顶点。

那么回路秩为

G = m – (n – 1)
= 7 – (5 – 1)
= 3

示例

设 G 为一个具有六个顶点的连通图，每个顶点的度数为三。求 G 的回路秩。

根据顶点度数之和定理，

6 × 3 = 2|E|

|E| = 9

回路秩 = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

Mahesh Parahar

更新于: 2019年8月23日

824 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习