干涉条件

---

简介

干涉条件是波动光学最重要的概念之一。光的现象、反射和折射只能基于波动光学来解释。光以波的形式传播的方向由光屏本身指示。当一块石头掉在静止的水面上时，涟漪会从石头掉落的地方向周围扩散。这个事件是波浪扩散的完美例子。当波纹经过某一点时，该点的水分子或粒子上下移动（或振荡）。与焦点等距的所有波节点都具有同相共振的波前。

干涉

• 当两列光波相互叠加时，某些点光强增加，其他点光强减弱的现象称为光的干涉。叠加是指光波的相加。

• 当两列波同时穿过介质时，合位移等于每列波对其施加的各个位移的矢量和。

• 根据相应波之间相位差的不同，合位移可以是最大值或最小值。

这些概念也适用于光。考虑来自两个光源$\mathrm{S_1}$和$\mathrm{S_2}$的光波，它们在点P处相遇。

来自光源$\mathrm{S_1}$的波在时间t到达P，

$$\mathrm{y_1=a_1\:sin\:ωt\:\:\:\:\:\rightarrow (1)}$$

来自光源$\mathrm{S_2}$的波在时间t到达P，

$$\mathrm{y_2=a_2 sin (\omega t+\phi)\:\:\:\:\:\rightarrow(2)}$$

这两列波具有不同的振幅$\mathrm{a_1}$和$\mathrm{a_2}$以及相似的角频率ω和相位差ϕ。这两列波引起的合位移

$$\mathrm{y=y_1+y_2=a_1 sin ωt+a_2 sin (\omega t+\phi)\:\:\:\:\:\rightarrow(3)}$$

使用三角恒等式求解此方程得到以下方程，

$$\mathrm{y=A sin (\omega t+\theta)\:\:\:\:\:\rightarrow(4)}$$

其中

$$\mathrm{A=\sqrt{a_1^2+a_2^2+2a_1 a_2\:cos\:\phi}\:\:\:\:\:\rightarrow(5)}$$

$$\mathrm{θ=tan^{-1}\frac{a_2\:sin\phi}{a_1+a_2 cos\phi}}$$

当$\mathrm{\phi=0,\pm 2\pi,\pm 4\pi,...}$时，合振幅最大。

$$\mathrm{A_{max}=\sqrt{(a_1+a_2 )^2}}$$

当$\mathrm{\phi =\pm \pi,\pm 3\pi,\pm 5\pi,...}$时，合振幅最小。

$$\mathrm{A_{max}=\sqrt{(a_1-a_2 )^2}}$$

强度与振幅的平方成正比

$$\mathrm{I \propto A^2\: \:\:\:\:\:\rightarrow(6)}$$

从公式(5)

$$\mathrm{I=I_1+I_2+2\sqrt{(I_1 I_2 )}cos \phi \:\:\:\:\:\:\rightarrow(7)}$$

干涉类型

相长干涉

• 当一个波的波峰与另一个波的波峰重叠时，它们的振幅相加，产生相长干涉，并且振幅大于各个波的振幅。

• 如果在某一点发生相长干涉，则该点的光强更大。

相消干涉

当一个波的波峰与另一个波的波谷重叠时，就会发生相消干涉。在发生相消干涉的点，光强最小。

干涉条件

• 在公式$\mathrm{I=I_1+I_2+2\sqrt{(I_1 I_2 )}cos \phi}$中，相位差$\mathrm{\phi=0,\pm 2π,\pm 4π,...}$是光强最大的条件。如果这两列波在此相位差下重叠，则会发生相长干涉。

• 在公式$\mathrm{I=I_1+I_2+2\sqrt{(I_1 I_2 )}cos\: \phi}$中，相位差$\mathrm{\phi=\pm π,\pm 3π,\pm 5π,...}$是光强最小的条件。

• 如果$\mathrm{a_1=a_2=a}$，则公式$\mathrm{A=\sqrt{a_1^2+a_2^2+2a_1 a_2 cos \:\phi}}$变为

$$\mathrm{A=\sqrt{2a^2+2a^2 cos \phi}=\sqrt{2a^2 (1+cos\phi\: ϕ}}$$

$$\mathrm{A=\sqrt{2a^2 2cos^2 (\phi /2)}}$$

$$\mathrm{A=2acos(\phi /2)}$$

$$\mathrm{I\propto 4a^2 cos^2 (\phi/2)\:\:\:\:[I\propto A^2]}$$

$$\mathrm{I=4I_0cos^2 (\phi/2)\:\:\:\:[I_0\propto a^2]}$$

如果$\mathrm{I_{max}=4I_0, ϕ=0,±2π,±4π .....,}$

如果$\mathrm{I_{max}=0, ϕ=±π,±3π,±5π .....,}$

由此可见，两列光波之间的相位差ϕ决定了交点处的强度。

薄膜干涉

• 考虑折射率为μ、厚度为d的薄膜。一束平行光以入射角i照射到薄膜上。

• 在光的入射点，它被分成两部分，反射部分和折射部分。

• 折射区域进入薄膜，并在薄膜底部进一步分成两部分。

• 另一部分在薄膜内部反射。由于薄膜多次发生内反射，因此会形成更多的反射和折射区域。通过薄膜反射和透射的光波产生单独的干涉。

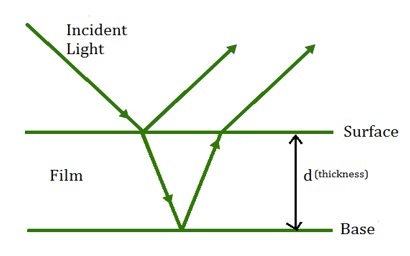
薄膜干涉

透射光的干涉

透射光波引起干涉并给出合强度。路程差为$\mathrm{\delta =2\mu d}$

由于透射光引起的相长干涉的条件是

$$\mathrm{2\mu d =n\lambda}$$

类似地，由于透射光引起的相消干涉的条件是

$$\mathrm{2\mu d =(2n-1)\frac{\lambda}{2}}$$

反射光的干涉

理论和实验都证明，穿过稀疏介质并被致密介质反射的光具有π的相位差。

反射光必须具有$\mathrm{\frac{λ}{2}}$的额外路程差。路程差为$\mathrm{\delta =2\mu d}$

由反射光引起的相长干涉的条件是

$$\mathrm{2μd+\frac{λ}{2}=nλ}$$

由反射光引起的相消干涉的条件是

$$\mathrm{2μd+\frac{λ}{2}=(2n+1)\frac{λ}{2}}$$

复色光中的干涉

• 在复色光（白光）中进行的干涉会导致屏幕上出现不同颜色的线条。

• 这是因为不同的颜色具有不同的波长。但是，中心线始终颜色明亮且为白色。

• 这是因为所有落在中心O上的颜色都具有零路程差。因此，对于所有颜色，只有相长干涉在O点发生，并且中心看起来很亮。

结论

光的现象、反射和折射只能基于波动光学来解释。当两列光波相互叠加时，某些点光强增加，其他点光强减弱的现象称为光的干涉。叠加是指光波的相加。在复色光（白光）中进行的干涉会导致屏幕上出现不同颜色的线条。这是因为不同的颜色具有不同的波长。如果在某一点发生相长干涉，则该点的光强更大。

常见问题

Q1. 解释光的散射

答：散射或电磁辐射的散射是指光波在穿过光介质、介质中的缺陷或与另一种介质的界面时，以意想不到的方向散射的现象。

Q2. 什么是负折射？

答：如果具有方向性和均匀特性的材料介质的磁导率和介电常数具有负值，则该介质中的光折射将为负值，这与超材料不同。

Q3. 什么是衍射？

答：波在障碍物边缘弯曲并进入障碍物几何阴影的现象称为衍射。衍射是包括声波在内的所有波的共同特性。

Q4. 为什么水上的油膜和肥皂泡会呈现出迷人的颜色？

答：这些颜色的原因是白光射线在薄膜的表面和底部之间多次反射而产生的干涉。这些颜色取决于光的入射角、薄膜的折射率和薄膜的厚度。

Q5. 定义相干光源

答：为了使两个波源成为相干光源，它们必须产生具有相同相位差或相同相位的波。此外，这两个波源必须产生相同频率或波长的波（单色）。