相消干涉方程

---

介绍

相消干涉是基于波叠加的概念。波是在介质中传播能量而不传播质量的扰动。波通常处于周期性运动中，就像一个简单的谐振子。它们有波峰和波谷。波的振幅是波的高度。两个连续波峰之间所覆盖的距离称为波长。每秒钟经过的波数称为波的频率。相位不是波的属性，但它给出了两个具有相同频率的信号之间的关系。粒子是一个局域化的物体，它拥有物理和化学性质，例如体积、质量、密度等。它们的大小可能不同，例如亚原子粒子、微观粒子和大块物质。

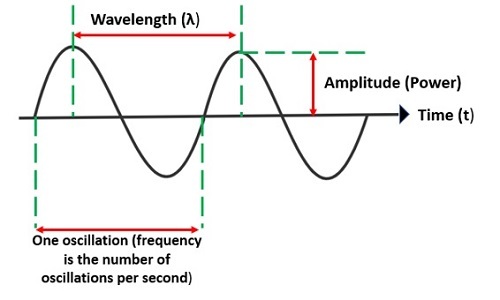
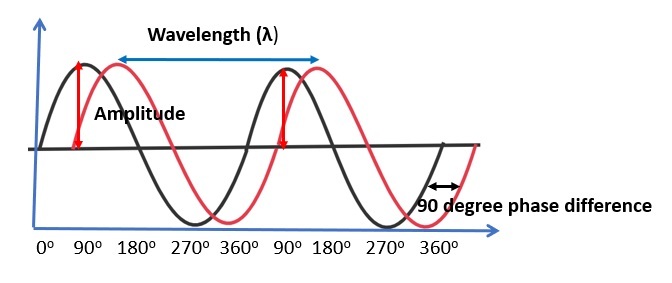
什么是波的干涉？

干涉是波叠加的现象。当两列波在同一介质中传播时，它们会相互干涉，这被称为波的干涉。当两列波叠加时，它们的振幅在每个点上都会相加，形成一个合波。合波可能具有较低、较高或相同的振幅。干涉效应适用于不同的波，例如光波、无线电波、声波和水波。波的干涉分为两种类型：相长干涉和相消干涉。

什么是相消干涉？

当两列即将相互作用的波的波峰相位差为180度时，一列波的位移为正，另一列波的位移为负。因此，在相互作用过程中，每列波的位移相互抵消。当第一列波的振幅上升时，第二列波的振幅下降，反之亦然。由于两列波的振幅在每个点上相互抵消，因此合波实际上没有波。

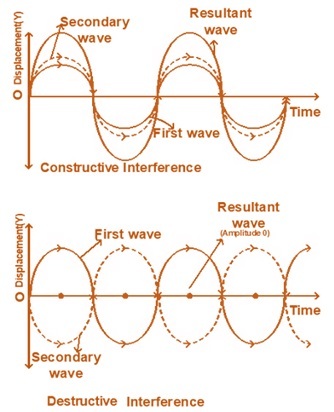
干涉最重要的条件至少是出现两列波。具有相同振幅和频率的波可以叠加并发生干涉。如果两列频率相当的波相互叠加，则合波的强度不同于总强度。合波的强度在不同的点上是不同的。

相消干涉方程

两列波之间的干涉可以用下面的数学公式表示。让我们考虑两列在同一介质中具有相同振幅的波。沿正X方向传播的波的方程为：

$$\mathrm{Y_1=Acos(kx-\omega t)}$$

其中A表示振幅

k表示波数，$\mathrm{k=\frac{2π}{λ}}$

λ表示波长。

ω表示角频率，ω=2πf

让我们取第二列波，它具有一定的相位差，并具有相同的振幅和频率。第二列波的方程为：

$$\mathrm{Y_2=Acos(kx-\omega t+\varphi)}$$

叠加时，振幅相加。

$$\mathrm{Y_1+Y_2=Acos(kx-\omega t)+Acos(kx-\omega t+\varphi)}$$

$$\mathrm{ Y_1+Y_2=A[cos(kx-\omega t)+cos(kx-\omega t+\varphi)]}$$

$$\mathrm{cos A +cos B=2cos(\frac{A-B}{2})cos(\frac{A+B}{2})}$$

所以，

$$\mathrm{Y_1+Y_2=2A[cos(\frac{kx-\omega t-kx+\omega t+\varphi}{2}) cos(\frac{kx-\omega t+kx-\omega t+\varphi}{2})]}$$

$$\mathrm{Y_1+Y_2=2A[cos(\frac{φ}{2}) cos(kx-ωt-\frac{φ}{2})]}$$

相长干涉

对于相长干涉，相位差是π的偶数倍。φ=0, 2π, 4π 等。所以$\mathrm{cos(\frac{φ}{2})=1}$。合波的振幅加倍。

$$\mathrm{Y_1+Y_2=2A cos(kx-\omega t)}$$

相消干涉

对于相消干涉，相位差是π的奇数倍。φ=π, 3π, 5π 等。所以$\mathrm{cos(\frac{φ}{2})=0}$。合波的振幅为零。

相消干涉的例子

下面给出一些相消干涉的例子。

• 运动的电子和无线电波也会导致相消干涉。对于运动的电子来说，相消干涉很容易发生，并且可以遵循相消干涉规则。

• 在降噪耳机中，相消干涉是一个重要因素。由于播放声音时声波的振幅方向相反，因此会发生相消干涉，它们相互抵消，从而降低噪音。

• 引力波就是一个相消干涉的例子。由于引力波在不同地点的传播速度不同，因此很难找到参考系。这就是在那里发生相消干涉的原因。

• 光束也是相消干涉的例子。

• 汽车消声器也是相消干涉的例子。通常也称为消音器。因此，它安装在任何车辆上以消除噪音。

• 大多数乐器都是相消干涉的例子。

• 扬声器波也会发生相消干涉。

结论

介质中传递能量的扰动称为波。衍射、干涉和偏振等现象表明光表现得像波。当两列波叠加时，它们会形成干涉波。根据叠加方式，波的干涉分为两种：相消干涉和相长干涉。当两列相同振幅的波相位差为180度时，它们的相反振幅相互抵消，合波的振幅为零。本教程还详细讨论了相消干涉方程及其一些例子。

常见问题

1.波的特性是什么？

波的特性如下。

• 振幅 - 粒子在波中从平均位置所做的最大位移。

• 周期 - 波完成一次往复运动所需的时间。

• 波长 - 两个连续波峰或波谷之间的距离。

• 频率 - 每秒钟完成的往复运动次数。

• 速度 - 波每秒传播的距离。

2.什么是相长干涉？

如果两列波的波峰同相，则两列波的位移都为正或都为负。因此，在两列这样的波相互作用过程中，两列波的振幅相加，合波的振幅是两列波振幅之和。这被称为相长干涉。

3.什么是波数？

在光谱学中，波数定义为单位距离内的波数。它被称为空间波数，其测量单位为cm^-1。在理论物理学中，波数定义为单位距离内存在的弧度数。它被称为角波数。它表示为：

$$\mathrm{ k=\frac{2π}{λ}}$$

4.在相消干涉过程中会发生什么，它们的相位差和路程差是多少？

在相消干涉过程中，两列波以相互抵消的方式叠加。两列波的相位差是π的奇数倍。

$$\mathrm{波之间的相位差\: =\phi= (2n-1) \pi}$$

两列波的路程差是λ/2的奇数倍。

$$\mathrm{波之间的路程差\: =\Delta= (2n-1) λ/2.}$$

5.什么是波的叠加原理？

叠加原理也称为叠加特性。当两列波在同一平面内传播时，它们会发生叠加，合波的振幅是两列个体波的振幅之和。