圆锥曲线

---

简介

• 当一个固体表面如圆锥体被平面切割时，它会形成不同的截面，称为圆锥曲线。

• 根据平面与圆锥轴线相交的角度不同，圆锥曲线可以是圆、椭圆、抛物线和双曲线。

• 圆和椭圆是封闭的截面，而抛物线和双曲线不是封闭的，它们的曲线延伸到无穷大。

圆锥截面的定义

• 当一个二维平面与一个三维直圆锥相交时，在平面上形成的截面称为圆锥曲线。

• 平面以不同的角度与圆锥相交，形成不同的圆锥曲线，如圆、抛物线、椭圆和双曲线。不同的圆锥曲线有不同的参数和方程。

圆锥曲线的参数

除了焦点、准线和离心率之外，圆锥曲线还有其他一些参数。

• 准线 - 它是一条平行于准线的直线，并且必须经过圆锥曲线的焦点，称为圆锥曲线的准线。

• 焦参数 - 圆锥曲线焦点到其对应准线的距离称为焦参数。

• 主轴 - 经过抛物线的焦点和准线的直线，或连接双曲线和椭圆两个焦点的直线称为主轴。其中点是圆锥曲线的中心。

• 线性离心率 - 圆锥曲线中心到焦点的距离称为圆锥曲线的线性离心率。

• 长轴 - 经过中心的弦中最长的称为长轴。

• 短轴 - 经过中心的弦中最短的称为短轴。

焦点、离心率和准线

• 准线 - 平面上一个动点到一个定点和一条定直线的距离的轨迹是定义圆锥曲线的另一种方法。这条定直线称为圆锥曲线的准线。

• 焦点 - 这个定点称为圆锥曲线的焦点。圆锥曲线的焦点不在其准线上。

• 离心率 - 考虑圆锥曲线上的一个点 P。点 P 到焦点的距离与点 P 到准线的垂直距离之比称为离心率，对于给定的圆锥曲线，它是常数。用'e'表示。

• 如果圆锥曲线的离心率为零，则它是圆。

• 如果圆锥曲线的离心率严格位于零和一之间，则它是椭圆。

• 如果圆锥曲线的离心率为一，则它是抛物线。

• 如果圆锥曲线的离心率大于一，则它是双曲线。

圆锥的截面

重要的圆锥曲线有圆、抛物线、椭圆和双曲线。

• 圆 - 当平面与圆锥的轴线成90度角切割时，就会形成一个名为圆的圆锥曲线。

• 椭圆 - 当平面与圆锥的轴线成小于90度但大于圆锥半顶角的角度切割时，就会形成一个名为椭圆的圆锥曲线。

• 抛物线 - 当平面与圆锥的轴线成等于圆锥半顶角的角度切割时，就会形成一个名为抛物线的圆锥曲线。

• 双曲线 - 当平面与圆锥的轴线成小于圆锥半顶角的角度切割时，就会形成一个名为双曲线的圆锥曲线。

圆锥截面的方程

四个圆锥曲线圆、椭圆、抛物线和双曲线都有各自的方程。

圆

圆是一组到一个称为圆心的点的距离相等的点的轨迹。这个距离称为圆的半径。根据距离，可以推导出圆的方程。

考虑一个圆心为 (p, q)，圆上有一点 P (x, y) 的圆。圆的半径为 r。

点 P 与圆心的距离等于半径 r。

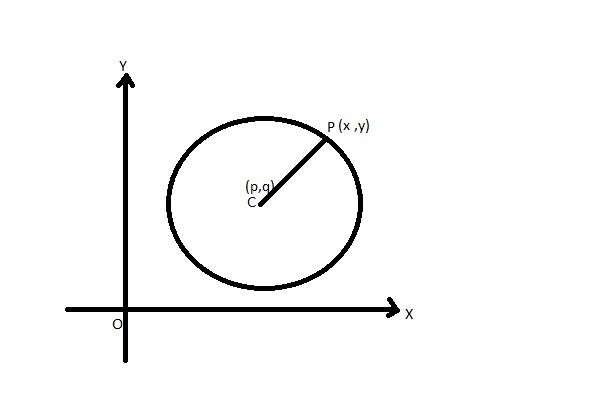
$\mathrm{(x\:-\:p)^{2}\:+\:(y\:-\:q)^{2}\:=\:r^{2}}$

椭圆

椭圆是一组到两个定点（称为焦点）的距离之和相等的点的轨迹。

考虑一个圆心为 (p, q)，椭圆上任意一点 (x, y)，长轴为 x 轴，a 为半长轴，b 为半短轴的椭圆。

$$\mathrm{\frac{(x\:-\:p)^{2}}{a^{2}}\:+\:\frac{(y\:-\:q)^{2}}{b^{2}}\:=\:1}$$

抛物线

抛物线是一组到焦点和到准线的垂直距离相等的点的轨迹。

考虑一个沿 x 轴，圆心为 (p, q)，抛物线上一点 P (x, y)，焦点在 (p + a, q) 的抛物线。

$$\mathrm{(y\:-\:p)^{2}\:=4a\:(x\:-\:p)}$$

双曲线

双曲线是一组到两个定点（称为焦点）的距离之差相等的点的轨迹。

考虑一个沿 x 轴，圆心为 (p, q)，双曲线上任意一点 (x, y)，a 为半实轴，b 为半虚轴的双曲线。

$$\mathrm{\frac{(x\:-\:p)^{2}}{a^{2}}\:-\:\frac{(y\:-\:q)^{2}}{b^{2}}\:=\:1}$$

示例

• 已知圆心为 (2, 3)，圆上有一点 P (x, y)，圆的半径为 4cm，求圆的方程？

$\mathrm{(x\:-\:2)^{2}\:+\:(y\:-\:3)^{2}\:=\:4^{2}}$

• 已知椭圆的方程为 $\mathrm{\frac{(x\:-\:1)^{2}}{16}\:+\:\frac{(y\:-\:2)^{2}}{9}\:=\:1}$，求椭圆的圆心、半长轴长度和半短轴长度？

将给定方程与 $\mathrm{\frac{(x\:-\:p)^{2}}{a^{2}}\:+\:\frac{(y\:-\:q)^{2}}{b^{2}}\:=\:1}$ 进行比较，椭圆的圆心等于 (1, 2)。

$\mathrm{a^{2}\:=\:16\Longrightarrow\:a\:=\:4\:,\:b^{2}\:=\:9\Longrightarrow\:b\:=\:3}$

结论

在本教程中，我们学习了圆锥曲线、其参数（如焦点、离心率、准线）、圆锥的不同截面（如圆、椭圆、抛物线、双曲线）及其方程。

常见问题解答

1. 以原点为中心的沿 x 轴的抛物线的方程是什么？

$\mathrm{y^{2}\:=\:4ax}$ 是以原点为中心的抛物线的方程。

2. 以原点为中心的圆的方程是什么？

如果原点是圆的圆心，则圆的方程是 $\mathrm{(x)^{2}\:+\:(y)^{2}\:=\:r^{2}}$

3. 圆锥曲线为双曲线的离心率条件是什么？

对于圆锥曲线为双曲线，其离心率必须大于一。

4. 已知双曲线圆心为 (-1, 4)，双曲线上有一点 P (x, y)，a = 5，b = 3，求双曲线的方程？

双曲线的方程是 $\mathrm{\frac{(x\:+\:1)^{2}}{25}\:-\:\frac{(y\:-\:4)^{2}}{9}\:=\:1}$

5. 以原点为中心的沿 y 轴的抛物线的方程是什么？

$\mathrm{x^{2}\:=\:4ay}$ 是以原点为中心的抛物线的方程。