从给定的 N 个节点的非循环图构建一棵素数二叉树

介绍

在编程和数据结构领域，二叉树被广泛用于高效地存储和检索数据。本文将探讨使用 C++ 代码从给定的由 N 个节点组成的非循环图构建素数二叉树的概念。二叉树可以从非循环图构建，此类图的类型包括树、有向无环图等等。素数树属于二叉树的一个分支，通过附加图的两个连续边来返回素数。

从给定的非循环图构建素数二叉树

素数二叉树是普通二叉搜索树 (BST) 的一个有趣变体。在 BST 中，每个节点有两个子节点：一个位于其左侧，值较小；另一个位于其右侧，值较大。素数二叉树采用了这个概念，但附加了一个约束条件：左子树中的每个节点都必须小于右子树中的任何节点。

示例

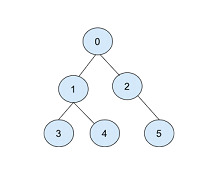
在上图的二叉树中，根节点选择为节点 0，它有两个子节点，左子节点为 1，右子节点为 2。左子节点进一步有两个子节点，分别为节点 3 和节点 4。由此构建的素数二叉树为 0 2 5。

方法 1：使用 C++ 代码从给定的 N 个节点的非循环图构建素数二叉树

我们首先包含必要的标准 C++ 库，例如 iostream。然后创建节点和图的类，以有效地表示结构。

算法

  • 步骤 1 − 创建一个 Node 类，其中包含三个成员：index、leftChild 和 rightChild。

  • 步骤 2 − 创建一个 createNode 函数，它接受一个整数参数并返回一个新节点，该节点具有给定的索引以及为空的左子节点和右子节点。

  • 步骤 3 − 创建 isprime() 函数来检查节点是否为素数。

  • 步骤 4 − 创建一个 printTree 函数，它接受指向二叉树根节点的指针并打印树的先序遍历。

  • 步骤 5 − 创建一个 constructPrimeBinaryTree 函数，它接受三个参数：图的邻接表的引用、已访问数组的引用以及当前节点的指针。该函数使用邻接表和已访问数组递归地构建具有素数的二叉树。对于当前节点的每个尚未访问的邻居，如果其索引加上当前节点的索引是素数，则创建一个具有邻居索引的新节点，如果当前节点的左子节点为空，则将其添加为左子节点，否则将其添加为右子节点。然后在新的节点上递归调用 constructPrimeBinaryTree()。

  • 步骤 6 − 在 main 中：

    • 将变量 n 初始化为 6，它是树中节点的数量。

    • 将变量 adjList 初始化为一个向量，该向量表示图的邻接表。

    • 将邻居添加到 adjList 的每个元素中。

    • 将变量 visited 初始化为一个向量，该向量表示节点是否已被访问。

    • 将 visited[0] 设置为 true，因为节点 0 是根节点。

    • 创建一个变量 root，它是一个指向使用 createNode(0) 函数创建的根节点的指针。

    • 调用 constructPrimeBinaryTree(adjList, visited, root) 函数，使用邻接表和已访问数组构建具有素数的二叉树。

    • 调用 printTree(root) 函数，以先序遍历方式打印树。

示例

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

class Node {
   public:
      int index;
      Node* leftChild;
      Node* rightChild;

      Node(int idx) : index(idx), leftChild(nullptr), rightChild(nullptr) {}
};

Node* createNode(int idx) {
   return new Node(idx);
}

bool isPrime(int n) {
   if (n <= 1)
      return false;
   for (int i = 2; i * i <= n; i++)
      if (n % i == 0)
         return false;
      return true;
}

void printTree(Node* root) {
   if (root == nullptr)
      return;

   cout << root->index << " ";
   printTree(root->leftChild);
   printTree(root->rightChild);
}

void constructPrimeBinaryTree(vector<vector<int>>& adjList, vector<bool>& visited, Node* curr) {
   for (int neighbor : adjList[curr->index]) {
      if (!visited[neighbor] && isPrime(curr->index + neighbor)) {
         visited[neighbor] = true;
         Node* newNode = createNode(neighbor);
         if (curr->leftChild == nullptr)
            curr->leftChild = newNode;
         else
            curr->rightChild = newNode;
            constructPrimeBinaryTree(adjList, visited, newNode);
      }
   }
}
int main() {
   int n = 6;

   vector<vector<int>> adjList(n);
   adjList[0].push_back(1);
   adjList[0].push_back(2);
   adjList[1].push_back(3);
   adjList[1].push_back(4);
   adjList[2].push_back(5);

   vector<bool> visited(n, false);
   visited[0] = true;
   Node* root = createNode(0);

   constructPrimeBinaryTree(adjList, visited, root);

   printTree(root);

   return 0;
}

输出

0 2 5

结论

本文探讨了如何使用 C++ 代码从给定的 N 个节点的非循环图构建素数二叉树。通过遵循上述逐步方法，程序员可以有效地在各种应用中实现这种数据结构。代码使用递归函数返回素数二叉树。

更新于: 2023-08-25

77 次浏览

开启您的 职业生涯

通过完成课程获得认证

立即开始
广告