数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学交替子数组计数
交替子数组计数用于计算没有两个相邻元素相同的子数组的数量。我们也可以将这些子数组称为交替子数组。
问题陈述
在了解什么是“交替子数组计数”之前，让我们先看看什么是子数组和交替子数组。
- 子数组是数组的一部分，通过移除数组的一些或所有前缀元素和一些或所有后缀元素形成。
-
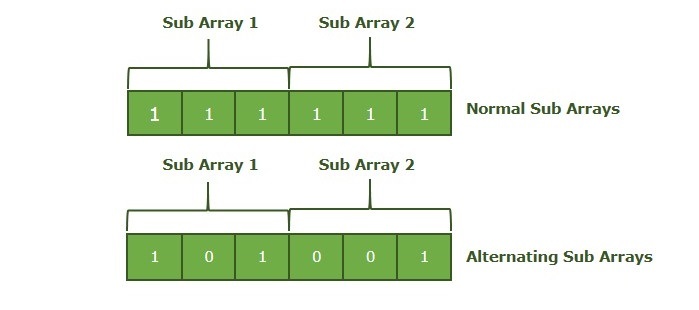
将数组分成多个子数组时，可能存在两个相邻子数组具有相同值的可能性。如果没有任何两个相邻子数组具有相同的值，则这些子数组被称为交替子数组。
示例场景 1
Input: nums = [1, 1, 1 , 1]
Output:count = 4
交替子数组 = [1]，[1]，[1]，[1]
示例场景 2
Input: nums = [1, 1, 1, 0]
Output:count = 5
交替子数组 = [1]，[1]，[1]，[0]，[1, 0]
示例场景 3
Input: nums = [1, 0, 1, 0, 1]
Output: count = 9
交替子数组 = [1]，[0]，[1]，[0]，[1]，[1, 0]，[0, 1]，[1, 0, 1]，[0, 1, 0]。
时间复杂度
计算交替子数组的时间复杂度为 O(n)，其中 (n) 是数组的长度。要使用各种编程语言解决此问题，请使用以下方法。
- 暴力法
- 动态规划法
暴力法
这种方法是解决所有可能的解决方案问题的直接方法。
示例
该程序通过迭代整数向量并添加所有交替子数组的长度来计算给定整数向量中交替子数组的数量。
#include <iostream>
#include <vector>
using namespace std;
class Count {
public:
long long countAlternatingSubarrays ( vector<int>& nums ) {
long long ans = 1, s = 1;
for (int i = 1; i < nums.size(); ++i) {
s = nums[i] != nums[i - 1] ? s + 1 : 1;
ans += s;
}
return ans;
}
};
int main() {
Count X;
vector<int> nums = {1, 0, 1, 0, 1, 0};
cout << " Count of alternating subarrays = " << X.countAlternatingSubarrays(nums) << endl;
return 0;
}
输出
Count of alternating subarrays = 21
import java.util.*;
public class Count {
public long countAlternatingSubarrays(int[] nums) {
long ans = 1, s = 1;
for (int i = 1; i < nums.length; ++i) {
s = (nums[i] != nums[i - 1]) ? s + 1 : 1;
ans += s;
}
return ans;
}
public static void main(String[] args) {
Count X = new Count();
int[] nums = {1, 0, 1, 0, 1, 0};
System.out.println("Count of alternating subarrays = " + X.countAlternatingSubarrays(nums));
}
}
输出
Count of alternating subarrays = 21
def count_alternating_subarrays(nums):
ans = s = 1
for i in range(1, len(nums)):
s = s + 1 if nums[i] != nums[i - 1] else 1
ans += s
return ans
nums = [1, 0, 1, 0, 1, 0]
print("Count of alternating subarrays =", count_alternating_subarrays(nums))
输出
Count of alternating subarrays = 21
动态规划法
此方法用于通过将复杂问题分解成更简单的子问题来解决复杂问题。
示例
以下是通过检查每个可能的子数组来计算给定整数向量中具有交替元素的子数组数量的程序。
#include <iostream>
#include <vector>
using namespace std;
long long countAlternatingSubarrays(const vector<int>& nums) {
long long count = 0;
for (int i = 0; i < nums.size(); ++i) {
int sign = 0;
for (int j = i; j < nums.size(); ++j) {
if (j == i || nums[j] != nums[j - 1]) {
count++;
sign = !sign;
} else {
break;
}
}
}
return count;
}
int main() {
vector<int> nums = {1, 0, 1, 0, 1, 0};
cout << "Count of alternating subarrays = " << countAlternatingSubarrays(nums) << endl;
return 0;
}
输出
Count of alternating subarrays = 21
import java.util.*;
public class Main {
public static long countAlternatingSubarrays(List <Integer> nums) {
long count = 0;
for (int i = 0; i < nums.size(); ++i) {
int sign = 0;
for (int j = i; j < nums.size(); ++j) {
if (j == i || !nums.get(j).equals(nums.get(j - 1))) {
count++;
sign = 1 - sign;
} else {
break;
}
}
}
return count;
}
public static void main(String[] args) {
List<Integer> nums = Arrays.asList(1, 0, 1, 0, 1, 0);
System.out.println("Count of alternating subarrays = " + countAlternatingSubarrays(nums));
}
}
输出
Count of alternating subarrays = 21
def count_alternating_subarrays(nums):
count = 0
for i in range(len(nums)):
sign = 0
for j in range(i, len(nums)):
if j == i or nums[j] != nums[j - 1]:
count += 1
sign = not sign
else:
break
return count
nums = [1, 0, 1, 0, 1, 0]
print("Count of alternating subarrays = ", count_alternating_subarrays(nums))
输出
Count of alternating subarrays = 21
更新于：2024年7月23日
浏览量：156
广告