数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究树中子树DFS的C++查询
在这个问题中，我们给定一棵二叉树，我们需要从一个特定的节点执行dfs，在这个节点中，我们假设给定的节点作为根节点并从中执行dfs。
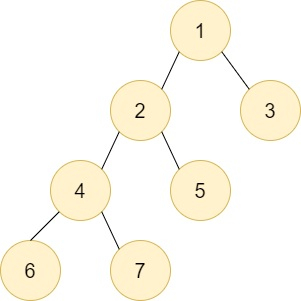
在上图中，假设我们需要从节点F执行DFS
在本教程中，我们将应用一些非正统的方法，以便它可以大大降低我们的时间复杂度，因此我们也能够为更高的约束运行此代码。
方法 - 在这种方法中，我们不会简单地走朴素的方法，即我们只是对每个节点应用dfs，因为它不适用于更高的约束，因此我们尝试使用一些非正统的方法来避免出现TLE。
#include <bits/stdc++.h>
using namespace std;
#define N 100000
// Adjacency list to store the
// tree nodes connections
vector<int> v[N];
unordered_map<int, int> mape; // will be used for associating the node with it's index
vector<int> a;
void dfs(int nodesunder[], int child, int parent){ // function for dfs and precalculation our nodesunder
a.push_back(child); // storing the dfs of our tree
// nodesunder of child subtree
nodesunder[child] = 1;
for (auto it : v[child]) { // performing normal dfs
if (it != parent) { // as we the child can climb up to
//it's parent so we are trying to avoid that as it will become a cycle
dfs(nodesunder, it, child); // recursive call
nodesunder[child] += nodesunder[it]; // storing incrementing the nodesunder
//by the number of nodes under it's children
}
}
}
// Function to print the DFS of subtree of node
void printDFS(int node, int nodesunder[]){
int ind = mape[node]; // index of our node in the dfs array
cout << "The DFS of subtree " << node << ": ";
// print the DFS of subtree
for (int i = ind; i < ind + nodesunder[node]; i++){ // going through dfs array and then
//printing all the nodes under our given node
cout << a[i] << " ";
}
cout << endl;
}
void addEdgetoGraph(int x, int y){ // for maintaining adjacency list
v[x].push_back(y);
v[y].push_back(x);
}
void mark(){ // marking each node with it's index in dfs array
int size = a.size();
// marks the index
for (int i = 0; i < size; i++) {
mape[a[i]] = i;
}
}
int main(){
int n = 7;
// add edges of a tree
addEdgetoGraph(1, 2);
addEdgetoGraph(1, 3);
addEdgetoGraph(2, 4);
addEdgetoGraph(2, 5);
addEdgetoGraph(4, 6);
addEdgetoGraph(4, 7);
// array to store the nodes present under of subtree
// of every node in a tree
int nodesunder[n + 1];
dfs(nodesunder, 1, 0); // generating our nodesunder array
mark(); // marking the indices in map
// Query 1
printDFS(2, nodesunder);
// Query 2
printDFS(4, nodesunder);
return 0;
}输出
The DFS of subtree 2: 2 4 6 7 5 The DFS of subtree 4: 4 6 7
理解代码
在这种方法中，我们预先计算dfs的顺序并将其存储在一个向量中，现在当我们预先计算了dfs时，我们还计算从每个节点开始的每个子树下存在的节点，然后我们简单地从该节点的起始索引遍历到其子树内所有节点的数量。
结论
在本教程中，我们解决了一个问题，以解决树中子树的DFS查询。我们还学习了此问题的C++程序以及解决此问题的完整方法（正常方法）。
我们可以用其他语言（如C、Java、Python和其他语言）编写相同的程序。希望本文对您有所帮助。
更新于： 2021年11月25日
289 次浏览
广告