数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究C++ 中 N 叉树的偶数大小子树
在这个问题中，我们得到一个邻接表，它表示一个 N 叉树。我们的任务是找到 *N 叉树中偶数大小子树的数量*。
N 叉树 **通常定义为节点的集合，通常以以下方式分层表示。**
树从根节点开始。
树的每个节点都维护一个指向其子节点的指针列表。
子节点的数量小于或等于 m。
让我们举个例子来理解这个问题，
输入：
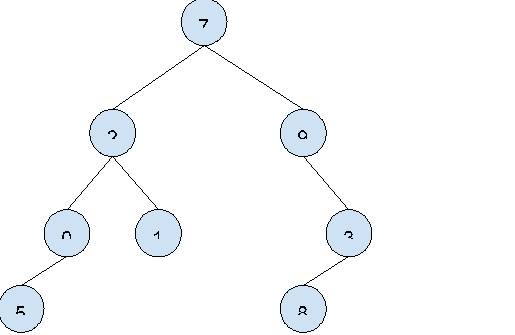
输出：4
解释：
以 7 为根的树具有偶数大小。
以 2 为根的树具有偶数大小。
以 0 为根的树具有偶数大小。
以 3 为根的树具有偶数大小。
解决方案方法 -
一个简单的方法是计算给定节点的所有子节点，如果它是偶数，则增加 evenTreeCount。为此，我们将使用 DFS，并找到给定节点的子树长度。
我们可以使用 *树上的单次遍历* 来做到这一点。通过递归地找到每个子节点的子树的大小，然后检查大小，如果它是偶数，则增加 evenTreeCount，否则保留它。
程序说明我们解决方案的工作原理，
示例
#include <bits/stdc++.h>
using namespace std;
int countEventSizeSubTree(vector<int> adj[], int n, int v, int& EvenCount){
int size = 1;
for (auto ele : adj[v]) {
size += countEventSizeSubTree(adj, n, ele, EvenCount);
}
if (size % 2 == 0)
EvenCount++;
return size;
}
int main(){
int n;
n = 10;
vector<int> adj[n + 1];
adj[7].push_back(2);
adj[7].push_back(9);
adj[2].push_back(0);
adj[2].push_back(1);
adj[9].push_back(3);
adj[3].push_back(8);
adj[0].push_back(5);
int EvenCount = 0;
countEventSizeSubTree(adj, n, 1, EvenCount);
cout<<"Even Size SubTree are "<<EvenCount;
return 0;
}输出 -
Even Size SubTree are 0
更新于： 2021 年 1 月 22 日
122 次浏览
广告