分流规则和分压规则

---

电路主要分为两种类型，即串联电路和并联电路，这取决于电路中组件的排列方式。串联电路是指组件串联连接的电路，而并联电路是指所有电路组件连接在两个公共点之间的电路。串联电路和并联电路分别充当分压电路和分流电路。阅读本文以了解更多关于分流规则和分压规则的信息。

分流规则

并联电路充当分流器，因为它将总电路电流分配到所有支路中。图1显示了一个分流电路，其中总电路电流I被分成电流I₁和I₂，分别流过具有电阻R₁和R₂的两个并联支路。我们可以注意到，两个电阻上的电压降相同，即V。

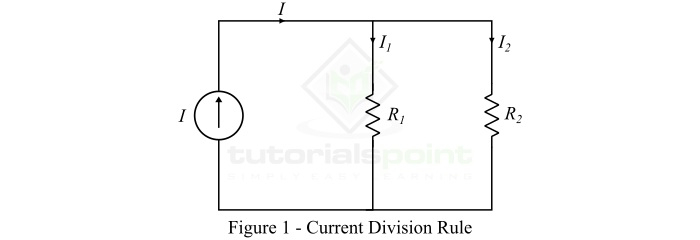
根据欧姆定律，

$$\mathrm{I_{1}=\frac{V}{R_{1}}\: 和\:I_{2}=\frac{V}{R_{2}} }$$

设R为电路的等效电阻，其计算公式为：

$$\mathrm{R=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\: \: \cdot\cdot\cdot\left ( 1 \right )}$$

此外，从电路图中，我们可以得到：

$$\mathrm{I=\frac{V}{R}=V\times \left ( \frac{R_{1}+R_{2}}{R_{1}R_{2}} \right )\: \:\cdot \cdot \cdot \left ( 2 \right )}$$

但是，我们知道两个电阻上的电压相同。

$$\mathrm{\therefore V=I_{1}R_{1}=I_{2}R_{2}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

因此，根据公式(2)和(3)，我们最终得到：

$$\mathrm{ I=I_{1}R_{1}\left ( \frac{R_{1}+R_{2}}{R_{1}R_{2}} \right )=I_{1}\left ( \frac{R_{1}+R_{2}}{R_{2}} \right )}$$

$$\mathrm{\therefore I_{1}=\frac{IR_{2}}{R_{1}+R_{2}}\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

类似地，

$$\mathrm{ I=I_{2}R_{2}\left ( \frac{R_{1}+R_{2}}{R_{1}R_{2}} \right )=I_{2}\left ( \frac{R_{1}+R_{2}}{R_{1}} \right )}$$

$$\mathrm{\therefore I_{2}=\frac{IR_{1}}{R_{1}+R_{2}}\cdot \cdot \cdot \left ( 5 \right )}$$

公式(4)和(5)给出了分流规则的表达式。根据这些公式，我们可以说，任何并联支路中的电流等于相反支路电阻与所有电阻之和的比率乘以总电路电流。

分压规则

串联电路充当分压器，因为它将总电源电压分配到电路元件上的不同电压。图2显示了一个分压电路，其中总电源电压V被分配到电阻R₁和R₂上的电压V₁和V₂。虽然两个电阻的电流相同，即I。

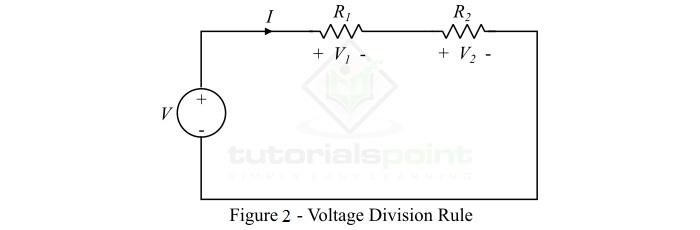
根据欧姆定律，

$$\mathrm{V_{1}=IR_{1}\: 和\: V_{2}=IR_{2}}$$

设R为电路的总电阻，其计算公式为：

$$\mathrm{R=R_{1}+R_{2}\: \: \: \cdot\cdot \cdot \left ( 1 \right ) }$$

此外，从电路图中，我们可以得到：

$$\mathrm{V=IR=I\left ( R_{1}+R_{2} \right )\: \: \: \cdot\cdot \cdot \left ( 2 \right ) }$$

但是

$$\mathrm{I=\frac{V_{1}}{R_{1}}=\frac{V_{2}}{R_{2}}\: \: \cdot \cdot \cdot \left ( 3 \right ) }$$

因此，根据公式(2)和(3)，我们最终得到：

$$\mathrm{V=\frac{V_{1}}{R_{1}}\left (R_{1}+R_{2}\right ) }$$

$$\mathrm{\therefore V_{1}=\frac{VR_{1}}{R_{1}+R_{2}}\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

类似地，

$$\mathrm{V=\frac{V_{2}}{R_{2}}\left (R_{1}+R_{2}\right ) }$$

$$\mathrm{\therefore V_{2}=\frac{VR_{2}}{R_{1}+R_{2}}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$

因此，根据分压规则公式，可以说，串联电路中电阻上的电压等于该电阻的值与总电源电压的乘积除以串联电阻的总电阻。

数值示例 (1)

求图3所示并联电路中的电流I₁和I₂。

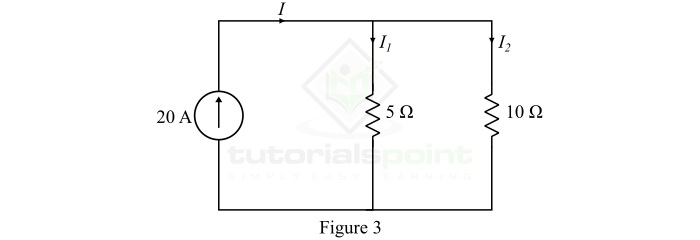
解答

使用分流规则，电阻R₁上的电流为：

$$\mathrm{I_{1}=I\times \frac{R_{2}}{R_{1}+R_{2}}=20\times \frac{10}{5+10}}$$

$$\mathrm{\therefore I_{1}=13.33\: A}$$

电阻R₂上的电流为：

$$\mathrm{I_{2}=I\times \frac{R_{1}}{R_{1}+R_{2}}=20\times \frac{5}{5+10}}$$

$$\mathrm{\therefore I_{2}=6.67\: A}$$

数值示例 (2)

求图4所示电路中电阻R₁和R₂上的电压。

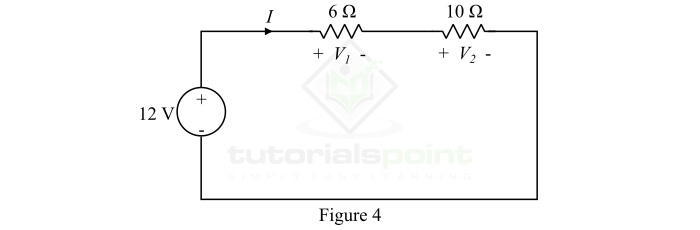
解答

使用分压规则，电阻R₁上的电压为：

$$\mathrm{V_{1}=\frac{VR_{1}}{R_{1}+R_{2}}=\frac{12\times 6}{6+10}= 4.5 V}$$

电阻R₂上的电压为：

$$\mathrm{V_{2}=\frac{VR_{2}}{R_{1}+R_{2}}=\frac{12\times 10}{6+10}= 7.5 V}$$

总结

以下几点总结了我们在本文中讨论的内容：

• 并联电路充当分流电路，因为它将总电路电流分配到所有支路中。

• 串联电路充当分压电路，因为它将总电源电压分配到电路的不同组件上。

• 分流规则指出，并联电路中任何并联支路上的电流等于相反支路电阻与所有电阻之和的比率乘以总电流。

• 分压规则指出，串联电路中任何串联组件上的电压等于该电阻的值与总电源电压的乘积除以串联电路的总电阻。