数据库管理系统 - 范式化

函数依赖

函数依赖 (FD) 是关系中两个属性之间的一组约束。函数依赖表示如果两个元组在属性 A1、A2、…、An 上具有相同的值，则这两个元组必须在属性 B1、B2、…、Bn 上具有相同的值。

函数依赖用箭头符号 (→) 表示，即 X→Y，其中 X 函数决定 Y。左侧属性决定右侧属性的值。

阿姆斯特朗公理

如果 F 是一组函数依赖，则 F 的闭包，记作 F⁺，是由 F 逻辑上隐含的所有函数依赖的集合。阿姆斯特朗公理是一组规则，重复应用这些规则可以生成函数依赖的闭包。

自反规则 − 如果 α 是一组属性，而 β 是 α 的子集，则 α 包含 β。
增广规则 − 如果 a → b 成立，而 y 是属性集，则 ay → by 也成立。也就是说，在依赖中添加属性不会改变基本依赖。
传递规则 − 与代数中的传递规则相同，如果 a → b 成立且 b → c 成立，则 a → c 也成立。a → b 称为函数决定 b。

平凡函数依赖

平凡的 − 如果函数依赖 (FD) X → Y 成立，其中 Y 是 X 的子集，则称为平凡的 FD。平凡的 FD 总是成立的。
非平凡的 − 如果函数依赖 (FD) X → Y 成立，其中 Y 不是 X 的子集，则称为非平凡的 FD。
完全非平凡的 − 如果函数依赖 (FD) X → Y 成立，其中 X 与 Y 的交集 = Φ，则称为完全非平凡的 FD。

范式化

如果数据库设计不完善，则可能包含异常，这对任何数据库管理员来说都像是一场噩梦。管理包含异常的数据库几乎是不可能的。

更新异常 − 如果数据项分散且未正确链接到彼此，则可能导致奇怪的情况。例如，当我们尝试更新一个数据项时，它的副本分散在多个位置，一些实例被正确更新，而另一些实例保留旧值。此类实例会使数据库处于不一致状态。
删除异常 − 我们试图删除一条记录，但由于不知道数据也保存在其他地方，一部分记录未被删除。
插入异常 − 我们试图在一个根本不存在的记录中插入数据。

范式化是一种消除所有这些异常并将数据库置于一致状态的方法。

第一范式

第一范式在关系（表）的定义中定义。此规则定义关系中的所有属性都必须具有原子域。原子域中的值是不可分割的单元。

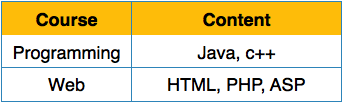
我们将关系（表）重新排列如下，以将其转换为第一范式。

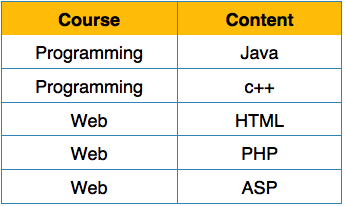
每个属性必须仅包含来自其预定义域的单个值。

第二范式

在学习第二范式之前，我们需要了解以下内容：

主键属性 − 作为候选键一部分的属性称为主键属性。
非主键属性 − 不是主键一部分的属性称为非主键属性。

如果我们遵循第二范式，则每个非主键属性都应完全函数依赖于主键属性。也就是说，如果 X → A 成立，则 X 的任何真子集 Y 都不能使 Y → A 也成立。

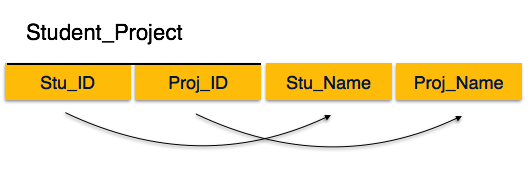
我们在 Student_Project 关系中看到，主键属性是 Stu_ID 和 Proj_ID。根据规则，非键属性，即 Stu_Name 和 Proj_Name 必须依赖于两者，而不能单独依赖于任何主键属性。但是我们发现 Stu_Name 可以独立地由 Stu_ID 识别，Proj_Name 可以独立地由 Proj_ID 识别。这称为部分依赖，第二范式不允许这种情况。

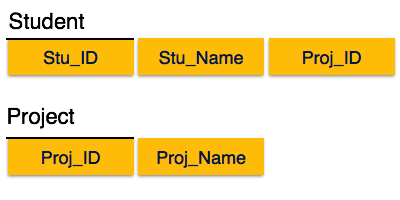
我们如上图所示将关系分解为两个。因此不存在部分依赖。

第三范式

为了使关系处于第三范式，它必须处于第二范式，并且必须满足以下条件：

任何非主键属性都不传递依赖于主键属性。
对于任何非平凡函数依赖 X → A，则：
- A 是主键属性。

我们发现在上面的 Student_detail 关系中，Stu_ID 是键并且是唯一的主键属性。我们发现 City 可以由 Stu_ID 和 Zip 本身识别。Zip 既不是超键，City 也不是主键属性。此外，Stu_ID → Zip → City，所以存在传递依赖。

为了将此关系转换为第三范式，我们将关系分解为两个关系，如下所示：

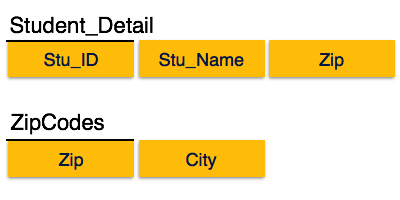
Boyce-Codd范式

Boyce-Codd 范式 (BCNF) 是对第三范式的严格扩展。BCNF 指出：

对于任何非平凡函数依赖 X → A，X 必须是超键。

在上图中，Stu_ID 是 Student_Detail 关系中的超键，Zip 是 ZipCodes 关系中的超键。所以，

Stu_ID → Stu_Name，Zip

和

Zip → City

这证实了这两个关系都处于 BCNF。

打印页面