德布罗意关系

---

简介

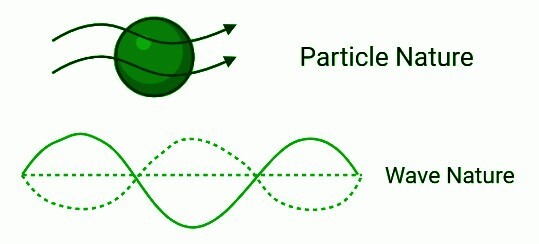
路易斯·德布罗意于 1924 年发表了他的研究成果，他提出电子 (e^-) 既具有波的性质也具有粒子的性质，就像光一样。他重新组织了普朗克-爱因斯坦关系的条件，以便它们可以应用于所有类型的物质。这种性质已被解释为物质的波粒二象性。他根据自己的发现推导出了物质动量与波长之间的关系。这种类型的关系被称为德布罗意关系。玻尔模型没有解释许多与众多原子光谱相关的概念，以及磁场和电场 (e.f.) 中光谱线的分裂。为了应对玻尔原子模型的挑战，人们采取措施创建了一个更全面的原子模型。每个运动的物体都具有波状外观。由于它们的质量很大，与普通物体相关的波长很短。因此，它们的波特性无法识别。另一方面，与电子或其他亚原子粒子相关的波长可以通过实验数据识别。

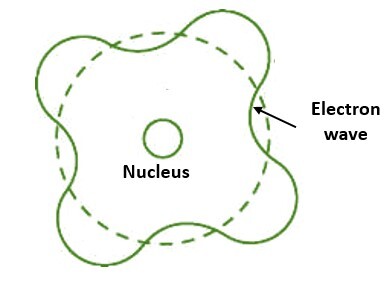
什么是德布罗意方程

德布罗意方程 (eq.) 是一个用于解释物质波属性的方程，特别是电子的波性质 (e^-)：λ=h/mv，其中 λ 是波长，h 是普朗克常数，m 是以速度 v 运动的粒子的质量。他提出粒子可以表现出波的特性。当乔治·佩吉特·汤姆逊的阴极射线衍射研究以及戴维森-革末研究中观察到物质波时，该研究适用于电子 (e^-)，德布罗意假设得到了证实。从那时起，已经证明德布罗意方程 (eq.) 适用于基本粒子、中性原子以及分子。

德布罗意方程的意义

根据德布罗意，所有运动的质量都具有其粒子性质。但是，运动中的汽车或球似乎没有粒子性质。为了证明这一点，德布罗意计算了板球的波长。

假设，

$$\mathrm{球的质量 = 150g (150 ✕ 10^{-3}kg),}$$

速度 = 35 m/s，并且

$$\mathrm{h=6.626 ✕ 10^{-34}Js}$$

现在，将这些数字代入方程

$$\mathrm{λ= hmv}$$

$$\mathrm{λ=6.626 ✕ 10^{-34}/150 ✕ 10^{-3}✕ 35 }$$

我们得到，

$$\mathrm{λ\: 球=1.2621✕ 10^{-34}} $$

$$\mathrm{m=1.2621 ✕ 10^{-24} Å}$$

因为 Å 是一个非常小的单位，所以该值以 10^-24 的幂表示。从现在开始，运动的板球是一个粒子。现在的问题是这个球是否具有波的性质。由于球的值是不可测量的，所以结果将是否定的。因此，德布罗意的波粒二象性理论适用于运动中的物体“直到”但不等于电子的尺寸。

电子的德布罗意波长

$$\mathrm{已知，m_e =9.1 ✕ 10^{-31} kg，\: v_e=218 ✕ 10^6 m/s }$$

将这些值代入公式

$$\mathrm{λ=h/mv=9.1 ✕ 10^{-31}/218 ✕ 10^6}$$

$$\mathrm{λ=3.2 Å }$$

此值是可量化的。因此，电子 (e^-) 具有波粒二象性。此外，所有大型物体都具有波的性质，而微观物体（如电子 (e^-)）则具有波粒二象性。

德布罗意假设的结论

德布罗意的理论是违反经典力学定律并为量子力学奠定基础的原因之一。每个运动的粒子都与其相关的波长相关联，这描述了物质的二元行为。该方程 (eq.) 的几种用途在化学领域以及物理学领域都有很好的依据。

我们可以从粒子的德布罗意方程 (eq.) 中推导出，即

λ=h/p=h/mv，

我们得出结论 -

如果 v=0，则 λ=∞，并且，

如果 λ=∞，则 v=0

这意味着波仅与运动的物质粒子相关联。因此，这些波的电荷不受影响。

结论

任何物质物体行为或属性的组成部分，如果根据描述波的数学方程 (Eqs.) 在空间或时间上发生变化，则称为德布罗意波，也称为物质波。德布罗意波方程 (Eqs.) 可用于确定任何运动物体的波长。电子的波长 (e^-) 随着其速度的降低而增加。他建立了波长与粒子动量 (p) 之间的特定关系。λ=h/mv=h/p。这里给出了波长，动量由 p 给出。每个运动的物体都具有波的性质。由于质量很大，与普通物体相关的波长非常短，以至于它们的波属性无法定义。

常见问题

1. 对于相同的德布罗意波长，电子 (e^-) 或质子哪个速度更快？

粒子具有相同的德布罗意波长。因此，它们的动量将相等。质量和速度的乘积是动量。因此，粒子的速度与其质量成反比。质量较大的质子将移动得更快，而质量较小的电子 (e^-) 将移动得更快。

2. 给出物体的德布罗意波长与动能之间的关系。

以动能 K 运动的电子的德布罗意波长 (e^-) 表示为，$\mathrm{λ=h/\sqrt{2mk}} $。根据德布罗意，与运动电子 (e^-) 相关的波的波长与其动量之间的关系为 λ=h/mv。德布罗意建立了物体波长与其动量之间的关系。连接是，λ=h/mv=h/p

3. 确定德布罗意波长与温度之间的关系。

我们知道粒子的平均 KE 为 -

K=3/2 k_bT

其中 k_b表示玻尔兹曼常数，T 表示开尔文温度。

粒子的动能为 $\mathrm{\frac{1}{2}}$ mv²

$$\mathrm{粒子的动量 p=mv=\sqrt{2mk} = \sqrt{2m(3/2)} k_b T=\sqrt{2mk_b T}} $$

$$\mathrm{德布罗意波长，A=h/p=h\sqrt{2mk_b T}} $$

4. 德布罗意假设是否适用于宏观物质？

德布罗意关系适用于微观物体和宏观物体。例如，一辆以 100m/s 速度行驶的 100Kg 的宏观汽车将具有

$$\mathrm{波长 λ=h/mv=6.63 \times 10^{-34}/100 \times 100=6.63 \times 10^{-30} m}$$

高能 -辐射的波长仅为 10^-12 m。

高频对应于非常小的波长。为了产生质量，特定波长以下或特定频率以上的波会产生粒子-反粒子湮灭。因此，在宏观物质中看不到波的性质或德布罗意波长。

5. 对于氢原子第 10 个玻尔轨道中的电子 (e^-)，德布罗意波长为 [h=6.625✕ 10^-34j/s，m_e=9.110✕ 10^-31 kg，a_0=0.529 Å]。

$$\mathrm{A_0=0.529 Å} $$

存在于 e^- 德布罗意的波长

$$\mathrm{第 1 个玻尔轨道 =2\Pi 0.529 Å} $$

$$\mathrm{第 10 个玻尔轨道 =2\Pi 0.529 Å10} $$

$$\mathrm{2\Pi 5.29 Å} $$

角动量的量子化

$$\mathrm{mva_0=h/2\Pi} $$

$$\mathrm{2\Pi a_0=h/mv=λ}$$

$$\mathrm{2\Pi a_0=2\Pi 5.29 Å} $$

$$\mathrm{=2\Pi 0.529 Å=33.2 Å} $$