数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究设计一个 NPDA 用于接受语言 L = {am b(2m) | m>=1}
基本上，一个下推自动机 (PDA) 如下所示：
“有限状态机 + 栈”
PDA 有三个组成部分，如下所示：
- 输入带。
- 控制单元。
- 一个无限大小的栈。
一个 PDA 可以正式地描述为七元组
(Q, Σ,S, δ,q0,I,F)
其中，
- Q 是有限数量的状态
- Σ 是输入字母表
- S 是栈符号
- Δ 是转移函数：QX(Σ∪{e})XSXQ
- q0 是初始状态 (q0 属于 Q)
- I 是初始栈顶符号
- F 是一组接受状态 (F 属于 Q)
问题
构造一个非确定性 PDA (NPDA) 用于接受语言
L = {am b2m | m>=1}。
解决方案
此语言生成的字符串为：
L = {abb, aabbbb, aaabbbbbb, aaaabbbbbbbb, ......}
该语言计算 a 的数量，然后是两倍数量的 b。
解释
步骤 1 - 保持 a 和 b 的顺序。
步骤 2 - 构建一个带有状态图的栈。
步骤 3 - a 和 b 的数量由栈维护。
步骤 4 - b 的数量正好是 a 的数量的两倍。
步骤 5 - 我们将使用 2 个栈字母
r = { a, z }
其中，
- r = 所有栈字母的集合
- z = 开始符号
给定问题的 PDA 构造
PDA 如下所示：
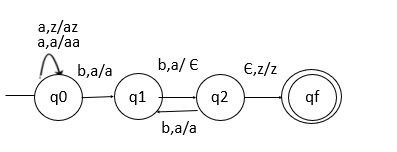
转移函数
PDA 的转移函数如下所示：
设计一个 NPDA，当 'a' 出现在 'b' 之前时将其压入栈中，如果再次出现 'a' 则再次压入。此外，当 'b' 出现时，从栈中弹出 'a'。
但我们对 b 的交替位置执行此弹出操作（对于两个 b 弹出一个 'a'，对于四个 b 弹出两个 'a'）。
最后，如果栈最终为空，则可以认为该字符串被 PDA 接受。
更新于：2021 年 6 月 15 日
601 次浏览
广告