设计一个下推自动机用于识别语言 L = {wwR | w ∈ {a, b}+}？

下推自动机用于实现上下文无关文法，就像我们使用某种技术为正则文法设计确定性有限自动机一样。DFA 使用有限的信息量工作，而 PDA 使用无限的信息量工作。

通常，下推自动机是：

"有限状态机" + "一个栈"

下推自动机包含三个组成部分：

  • 一个输入带；

  • 一个控制单元；以及

  • 一个无限大小的栈。

现在考虑一个问题：如何为给定的语言设计下推自动机？

问题

设计一个识别偶数长度回文串的下推自动机，用于语言 **L = {wwR | w ∈ {a, b}+}**。

解答

  • 读取字符串并将其保存到栈中。

  • 在每一步中，考虑您可能已到达中间点的可能性。

  • 一旦到达中点，就开始反向工作，如果匹配已保存的内容，则从栈中移除内容。

在每一步，我们都需要测试我们是否位于字符串的中间。

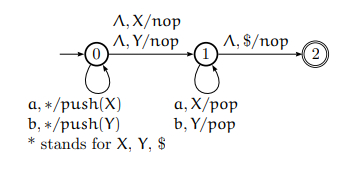
以下是字符串 **aabbaa** 的逐步瞬时描述：

  • 开始 → (0, aabbaa, $)

  • 加载栈 → (0, abbaa, X$)

  • 加载栈 → (0, bbaa, XX$)

  • 加载栈 → (0, baa, YXX$)

  • 尝试，这是中间点吗？ → (1, baa, YXX$)

  • 弹出栈 → (1, aa, XX$)

  • 弹出栈 → (1, a, X$)

  • 弹出栈 → (1, ∧, $)

  • 完成！ → (2, ∧, $)

更新于：2021年6月15日

7K+ 浏览量

开启你的职业生涯

完成课程获得认证

开始学习
广告