对角矩阵

---

引言

对角矩阵是指除了主对角线上的元素外，其他所有元素都为零的矩阵。矩阵应用于现实生活中的事件，例如军事阅兵、学校阅兵和种植。矩阵和行列式的概念被记录为出现在公元前四世纪，尽管其使用被认为仅始于公元前二世纪。然后，在十七世纪末，矩阵和行列式的概念重新使用。日常世界问题的数学模型被构成 为一组线性方程。矩阵对于解决这些问题是必不可少的。

矩阵

矩阵是用括号[ ]括起来的，按列和行排列的元素的矩形表示。

• 通常，矩阵的元素可以是实数、复数、单变量函数（即多项式函数、三角函数及其组合）和多变量函数。

• 具有m行和n列的矩阵A可以写成

$$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n},\:1\leq\:i\:\leq\:m\:,\:1\leq\:j\leq\:n,\:\:即}$$

$$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$$

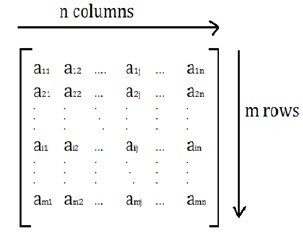
• 矩阵的阶或维数定义为$\mathrm{m\times\:n}$。即，m和n是矩阵中存在的行和列。

• 行定义为矩阵中的水平元素。列定义为矩阵中的垂直元素。

矩阵的类型

行矩阵和列矩阵

• $\mathrm{A\:=\:\begin{bmatrix} A\end{bmatrix}_{1\times\:4}\:=\:\begin{bmatrix} 1 & 0 & 1.1 & \sqrt{2}\\ \end{bmatrix}}$是一个阶数为1×4的行矩阵。因为这个矩阵的行总数为一。

• 如果$\mathrm{A\:=\:\begin{bmatrix} A\end{bmatrix}_{1\times\:4}\:=\:\begin{bmatrix} x \\ x\:+\:z \\ 3x \\ 4 \end{bmatrix}}$，则称为列矩阵。因为此矩阵的列总数为一。

零矩阵和非零矩阵

• 如果矩阵$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$中所有$\mathrm{1\leq\:i\leq\:m}$和$\mathrm{1\leq\:j\leq\:n}$的值都满足𝑎𝑖𝑗 = 0，则称为零矩阵，记作O。

• 如果矩阵A中的一个元素非零，则该矩阵称为非零矩阵。

方阵

• 行数和列数相同的矩阵称为方阵。也就是说，当一个n×n阶方阵时，方阵的阶数为n。例如

$$\mathrm{A\:=\:\begin{bmatrix} a & b & c \\ d & c & f\\ g & h & i \end{bmatrix}}$$

三角矩阵

• **上三角矩阵** - 方阵中主对角线以下的元素为零的矩阵。

• 因此，在方阵$\mathrm{B\:=\:\begin{bmatrix} b_{ij}\end{bmatrix}_{m\times\:n},\:如果\:b_{ij}\:=\:0,\:j\:<i.}$中，则该矩阵称为上三角矩阵。

$$\mathrm{B\:=\:\begin{bmatrix} 1 & 5 & 7 \\ 0 & 1 & 8\\ 0 & 0 & 2 \end{bmatrix}}$$

• **下三角矩阵** - 方阵中主对角线以上的元素为零的矩阵。

• 因此，在方阵$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n},\:如果\:a_{ij}\:=\:0,\:i\:<j.}$中，

$$\mathrm{B\:=\:\begin{bmatrix} 2 & 0 & 0 \\ 7 & 6 & 0\\ 3 & 3 & 9 \end{bmatrix}}$$

对角矩阵

• n阶方阵$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$的元素$\mathrm{a_{11}\:,\:a_{22}\:,\:a_{33}\:.............,a_{nn}}$称为**主对角线元素**。

• 除了主对角线元素外，其他元素都为零的矩阵称为对角矩阵。

• 对于所有$\mathrm{b_{ij\:=\:0\:,\:i\neq\:j}}$的方阵$\mathrm{B\:=\:\begin{bmatrix} b_{ij}\end{bmatrix}_{m\times\:n}}$称为对角矩阵。因此，在对角矩阵中，除了主对角线元素外，每个元素都为零。

对角矩阵的类型

数量矩阵

• 它定义为对角矩阵中每个主对角线元素都相同。

在方阵$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$中，如果$\mathrm{a_{ij}\:=\:c;i\:=\:j}$且$\mathrm{a_{ij}\:=\:0;\:i\neq\:j}$，则A为数量矩阵。这里c是一个常数。

$$\mathrm{A\:=\:\begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0\\ 0 & 0 & 2 \end{bmatrix}}$$

单位矩阵

• 单位矩阵 - 如果对角矩阵的每个元素都为零，除了主对角线元素为1。

在方阵$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$中，如果$\mathrm{a_{ij}\:=\:1;i\:=\:j}$ 且$\mathrm{a_{ij}\:=\:0;i\:\neq\:j}$，则矩阵A为单位矩阵。

$$\mathrm{I\:=\:\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}}$$

对角矩阵的性质

对角矩阵的加法和乘法非常简单。如果对角矩阵的主对角线元素（从左上角开始）为𝑎1，……，𝑎𝑛，则可以通过将矩阵写成diag(𝑎1，……，𝑎𝑛)来执行矩阵运算。两个对角矩阵的加法和乘法为

$$\mathrm{A\:=\:\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}\:\:\:B\:=\:\begin{bmatrix} c & 0 \\ 0 & d \end{bmatrix}}$$

$$\mathrm{A\:+\:B\:=\begin{bmatrix} a\:+\:c & 0 \\ 0 & b\:+\:d \end{bmatrix}}$$

$$\mathrm{AB\:=\:\begin{bmatrix} ac & 0 \\ 0 & bd \end{bmatrix}}$$

• **对角矩阵的转置**适用于每个主对角线元素都不为零的情况。

对角矩阵的应用

• 对角矩阵广泛应用于**线性代数**中。

• **线性映射**由对角矩阵表示。希望表示线性映射。

• 根据谱定理，对角矩阵与正规矩阵相似。

解题示例

1) 求矩阵X的值？

$$\mathrm{AX\:=\:B}$$

$$\mathrm{A\:=\:\begin{bmatrix} 7 & 0 & 0 \\ 0 & 12 & 0\\ 0 & 0 & 8 \end{bmatrix}\:\:X\:=\begin{bmatrix} x \\ y \\ z \end{bmatrix}\:\:B\:=\begin{bmatrix} 28 \\ 12 \\ 16 \end{bmatrix}}$$

答案

$$\mathrm{\begin{bmatrix} 7 & 0 & 0 \\ 0 & 12 & 0\\ 0 & 0 & 8 \end{bmatrix}\:\:\begin{bmatrix} x \\ y \\ z \end{bmatrix}\:\:=\:\begin{bmatrix} 28 \\ 12 \\ 16 \end{bmatrix}}$$

$$\mathrm{AX\:=\:\begin{bmatrix} 7x\:+\:0\:+\:0 \\ 0\:+\:12y\:+\:0 \\ 0\:+\:0\:+\:8z \end{bmatrix}}$$

$$\mathrm{AX\:=\begin{bmatrix} 7x \\ 12y \\ 8z \end{bmatrix}}$$

$\mathrm{AX\:=\:B}$，因此

$$\mathrm{7x\:=\:28}$$

$$\mathrm{12y\:=\:12}$$

$$\mathrm{8z\:=\:16}$$

$$\mathrm{x\:=\:4\:,\:y\:=\:1\:,\:z\:=\:2}$$

$$\mathrm{X\:=\begin{bmatrix} 4 \\ 1 \\ 2 \end{bmatrix}}$$

2) 证明矩阵A乘以单位矩阵将得到相同的矩阵？

$\mathrm{A\:=\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}}$

答案

$$\mathrm{A\:=\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}\:\:I\:=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}}$$

$$\mathrm{AI\:=\:\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}\:\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}}$$

$$\mathrm{AI\:=\:\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}}$$

因此，任何矩阵乘以单位矩阵都将得到相同的矩阵。

结论

矩阵应用于现实生活中的事件，例如军事阅兵、学校阅兵和种植。矩阵是用括号括起来的，按列和行排列的元素的矩形表示。如果矩阵A中的一个元素非零，则该矩阵称为非零矩阵。对角矩阵的加法和乘法非常简单。除了主对角线元素外，其他元素都为零的矩阵称为对角矩阵。对角矩阵的转置适用于每个主对角线元素都不为零的情况。对角矩阵广泛应用于线性代数中。线性映射由对角矩阵表示。希望表示线性映射。根据谱定理，对角矩阵与正规矩阵相似。

常见问题解答

1. 什么是正规矩阵？

• 如果一个方阵与其共轭转置矩阵的乘法是**可交换**的，则该矩阵称为**正规矩阵**。

• 实数元素的方阵，其共轭转置矩阵与其自身相同，因为每个元素的实数部分就是其自身。因此，所有实数元素的方阵都是正规矩阵。

2. 定义共轭转置矩阵？

复数元素矩阵的共轭转置矩阵是通过首先转置该矩阵，然后将转置矩阵的每个元素替换为其共轭复数而得到的。

3. 矩阵的秩是什么？

• 矩阵的子矩阵和子式是定义矩阵秩所必需的。

• 矩阵𝐵的秩是其非零子式行列式的最高阶数。

• 矩阵𝐵的秩记作⍴(𝐵)。零矩阵的秩为零。如果矩阵中至少存在一个非零元素，则$\mathrm{p(B)\:\geq\:1}$。

4. 矩阵的应用有哪些？

• 矩阵用于表示线性方程组的值。

• 矩阵编码及其函数用于在各个领域生成计算机电子表格，例如业务相关的预算编制、销售计划的定价以及分析科学实验的结果。

5. 解释矩阵的转置

通过转置矩阵𝐴的列和行而得到的矩阵称为𝐴的转置矩阵。它将标记为𝐴𝑇。也就是说，如果$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$，则$\mathrm{A^{T}\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{n\times\:m}}$。