无失真传输系统

---

失真定义为信号在通过系统传输时形状的变化。因此，当系统的输出是输入信号的精确复制时，信号通过系统的传输被认为是无失真的。此复制品，即系统的输出，可能具有不同的幅度，也可能具有不同的时间延迟。

输出信号幅度的恒定变化和恒定的时间延迟不被视为失真。只有信号形状的变化才被认为是失真。

数学上，如果系统的输出为，则信号𝑥(𝑡)的传输被认为是无失真传输。

$$\mathrm{y(t)=kx(t-t_{d})\; \; \cdot \cdot \cdot (1)}$$

其中，

• 常数k表示幅度的变化，无论是放大还是衰减。

• 𝑡_𝑑是延迟时间。

无失真系统的框图以及典型的输入和输出波形如图1所示。

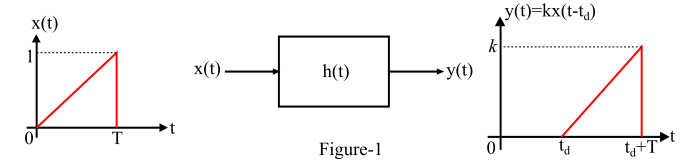
现在，对等式(1)两边进行傅里叶变换，并使用傅里叶变换的移位特性，我们得到，

$$\mathrm{Y(\omega )=ke^{-j\omega t_{d}}X\left ( \omega \right )}$$

因此，无失真传输系统的传递函数由下式给出，

$$\mathrm{H(\omega )=\frac{Y\left ( \omega \right )}{X\left ( \omega \right )}=ke^{-j\omega t_{d}}\; \; \cdot \cdot \cdot (2)}$$

现在，对等式(2)进行傅里叶逆变换，得到系统对应的冲激响应，

$$\mathrm{h(t)=k\delta (t-t_{d})\: \: \cdot \cdot \cdot (3)}$$

传递函数的幅度为，

$$\mathrm{\left | H(\omega ) \right |=k}$$

对于所有𝜔值，它都是常数。

传递函数的相移为，

$$\mathrm{\theta \left ( \omega \right )=\angle H(\omega )=-\omega t_{d}}$$

一般情况下，相移为，

$$\mathrm{\theta \left ( \omega \right )=n\pi -\omega t_{d};\; \; \left ( n\: is\:an\:integer \right )}$$

并且它随频率线性变化。图2显示了无失真传输系统的幅度和相位特性。

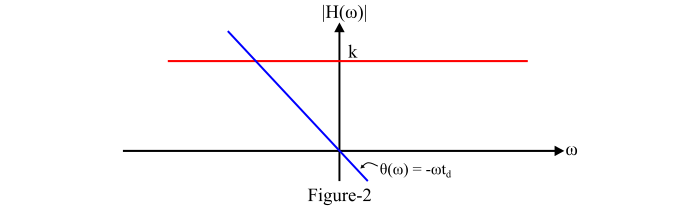
因此，为了使信号通过系统进行无失真传输，系统传递函数的幅度|𝐻(𝜔)|应为常数，即输入信号必须对所有频率分量进行相同的放大或衰减。因此，为了实现系统的无失真传输，系统的带宽是无限的，并且相位谱应与频率成正比。然而，在实践中，不存在带宽无限的系统，因此无失真传输的条件永远不会完全满足。