单相架空交流输电系统中所需的导体材料

单相交流输电系统

在电力传输系统中，使用两个导体（即相导体和中性线）来传输电力的系统被称为单相交流输电系统。

单相交流输电系统可分为以下三种类型：−

• 单相两线制系统，其中一根导线接地

• 单相两线制系统，其中中点接地

• 单相三线制系统

一相两线制系统（一根导线接地）所需的导体材料

图 1 显示了一根导线接地的单相两线制交流系统。

假设：

• $\mathrm{传输功率\mathrm{\, =\, }\mathit{P}}$

• $\mathrm{导体间最大电压\mathrm{\, =\, }\mathit{V_{m}}}$

• $\mathrm{电压的有效值\mathrm{\, =\, }\frac{\mathit{V{_m}}}{\sqrt{2}}}$

• $\mathrm{负载功率因数\mathrm{\, =\, }cos\, \phi }$

则负载电流由下式给出：

$$\mathrm{\mathit{I_{\mathrm{1}}\mathrm{\, =\, }\frac{P}{\frac{V_{m}}{\sqrt{\mathrm{2}}}\mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{\sqrt{\mathrm{2}P}}{V_{m}\, \mathrm{cos}\, \phi} } }$$

如果 a₁ 是每根导体的横截面积，则每根导体的电阻由下式给出：

$$\mathrm{\mathit{R_{\mathrm{1}}\mathrm{\, =\, }\frac{\rho \, l}{a_{\mathrm{1}}}}}$$

因此，线路损耗由下式给出：

$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{1}^{2}}\, R_{\mathrm{1}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{\mathrm{\sqrt{2}}P}{V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{1}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W \mathrm{\, =\, }\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi \,a_{\mathrm{1}}} }}}$$

$$\mathrm{\therefore 横截面积,\mathit{ a_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}}$$

现在，在单相两线制架空交流输电系统（一根导线接地）中所需的导体材料体积（假设为 K）由下式给出：

$$\mathrm{\mathit{K\mathrm{\, =\, }\mathrm{2}a_{\mathrm{1}}l\mathrm{\, =\, }\mathrm{2}\times \left (\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }\right )\times l}}$$

$$\mathrm{\mathit{\therefore K\mathrm{\, =\, }\frac{\mathrm{8}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}\, \, \, \cdot \cdot \cdot \left ( 1 \right )}$$

一相两线制系统（中点接地）所需的导体材料

图 2 显示了单相两线制交流输电系统，其中中点接地。

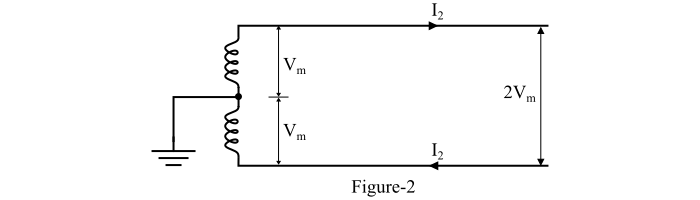
这里，两根导线相对于地具有相等且相反的最大电压 (V_m)。因此，两根导线之间的最大电压为 2V_m。

$$\mathrm{电压的有效值\mathit{\mathrm{\, =\, }\frac{\mathrm{2}V_{m}}{\mathrm{\sqrt{2}}}\mathrm{\, =\, }\sqrt{\mathrm{2}}V_{m}}}$$

$$\mathrm{负载电流,\mathit{I_{\mathrm{2}}\mathrm{\, =\, }\frac{P}{\sqrt{\mathrm{2}}V_{m}\, \mathrm{cos\, \phi}}} }$$

如果 𝑎₂ 是每根导体的横截面积，则传输线中的总功率损耗为

$$\mathrm{线路损耗,\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{2}^{2}}\, R_{\mathrm{2}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{\mathrm{\sqrt{2}}V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{2}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W \mathrm{\, =\, }\frac{P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi \,a_{\mathrm{2}}} }}}$$

$$\mathrm{\therefore 横截面积,\mathit{ a_{\mathrm{2}}\mathrm{\, =\, }\frac{P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}}$$

现在，在单相两线制架空交流输电系统（中点接地）中所需的导体材料体积（假设为 K₁）为：

$$\mathrm{\mathit{K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{2}a_{\mathrm{2}}l\mathrm{\, =\, }\mathrm{2}\times \left (\frac{P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }\right )\times l}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}\, \, \, \cdot \cdot \cdot \left ( 2 \right )}$$

比较公式 (1) 和 (2)，我们有：

$$\mathrm{\mathit{ \frac{K_{\mathrm{1}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )}{\mathrm{\mathit{\left ( \frac{\mathrm{8}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )}}}}\mathrm{\, =\, }\frac{1}{4}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }}0.25\times \mathit{K}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

因此，单相两线制交流系统（中点接地）所需的导体材料体积是单相两线制系统（一根导线接地）所需体积的 0.25 倍。

单相三线制系统所需的导体材料

图 3 显示了单相三线制交流系统。该系统由两根外线和一根从相绕组中点引出的中性线组成。当平衡负载连接到系统时，中性线中的电流为零。

参考电路，

• $\mathrm{导体间最大电压\mathrm{\, =\, }\mathit{\mathrm{2}V_{m}}}$

• $\mathrm{导体间电压的有效值\mathrm{\, =\, }\mathit{\frac{\mathrm{2}V_{m}}{\mathrm{\sqrt{2}}}\mathrm{\, =\, }\mathrm{\sqrt{2}}V_{m}}}$

• $\mathrm{负载功率因数\mathrm{\, =\, }cos\, \phi }$

则系统的负载电流由下式给出：

$$\mathrm{\mathit{I_{\mathrm{3}}\mathrm{\, =\, }\frac{P}{\sqrt{\mathrm{2}}V_{m}\, \mathrm{cos\, \phi}}} }$$

如果 a₃ 是每根外导体的横截面积，则

$$\mathrm{线路损耗,\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{3}^{2}}\, R_{\mathrm{3}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{\mathrm{\sqrt{2}}V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{3}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W \mathrm{\, =\, }\frac{P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi \,a_{\mathrm{3}}} }}}$$

$$\mathrm{\therefore 横截面积,\mathit{ a_{\mathrm{3}}\mathrm{\, =\, }\frac{P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}}$$

假设中性线的横截面积是外线的一半。则在单相三线制架空交流输电系统中所需的导体材料体积（假设为 K₂）由下式给出：

$$\mathrm{\mathit{K_{\mathrm{2}}\mathrm{\, =\, }\mathrm{2.5}a_{\mathrm{3}}l\mathrm{\, =\, }\mathrm{2.5}\times \left (\frac{P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }\right )\times l}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{2}}\mathrm{\, =\, }\frac{\mathrm{2.5}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}\, \, \, \cdot \cdot \cdot \left ( 4 \right )}$$

现在，比较公式 (1) 和 (4)，我们得到：

$$\mathrm{\mathit{ \frac{K_{\mathrm{2}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{2.5}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )}{\mathrm{\mathit{\left ( \frac{\mathrm{8}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )}}}}\mathrm{\, =\, }\frac{5}{16}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{2}}\mathrm{\, =\, }}\left ( \frac{5}{16} \right )\times \mathit{K}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$

因此，单相三线制架空交流输电系统所需的导体材料体积是单相两线制系统（一根导线接地）所需体积的 (5/16) 倍。

Manish Kumar Saini

更新于: 2022 年 2 月 24 日

1K+ 次查看

开启您的 职业生涯

通过完成课程获得认证

立即开始