地下直流系统所需的导体材料体积是多少？

地下直流系统

当直流电力通过地下电缆从发电站传输到用户时，该电力传输系统称为**地下直流系统**。

地下直流传输系统分为三种类型：

• 两线制直流系统

• 带中点接地的两线制直流系统

• 三线制直流系统

地下两线制直流系统所需的导体材料

地下两线制直流系统如图1所示。它有两根从发电机端子引出的导线。

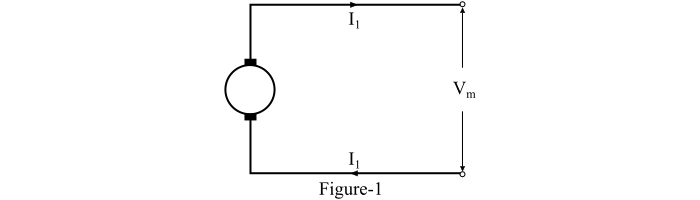
令：

• 𝑉_𝑚 = 导线间的最大电压

• 𝑃 = 要传输的功率

• 𝑙 = 传输功率的距离

负载电流由下式给出：

$$\mathrm{\mathit{I_{\mathrm{1}}\mathrm{\, =\, }\frac{P}{V_{m}}}}$$

如果𝑎₁是每根导线的横截面积，则每根导线的电阻为：

$$\mathrm{\mathit{R_{\mathrm{1}}\mathrm{\, =\, }\rho \frac{l}{a_{\mathrm{1}}}}}$$

系统中的总功率损耗由下式给出：

$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{1}^{2}}\, R_{\mathrm{1}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{V_{m}} \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{1}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}a_{\mathrm{1}}} }}$$

$$\mathrm{\therefore 横截面积,\mathit{ \: a_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} }}$$

因此，地下两线制直流系统所需的导体材料体积，设为K，由下式给出：

$$\mathrm{\mathit{ K\mathrm{\, =\, }\mathrm{2}a_{\mathrm{1}}l\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} \right )\times l}}$$

$$\mathrm{\mathit{\therefore K\mathrm{\, =\, }\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$

带中点接地的地下两线制直流系统所需的导体材料

带中点接地的地下两线制直流系统的电路图如图2所示。

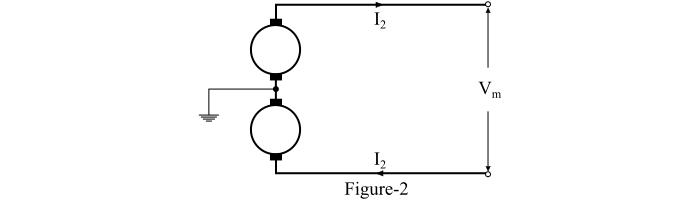
令：

• 𝑉_𝑚 = 导线间的最大电压
• 𝑃 = 要传输的功率

那么，负载电流由下式给出：

$$\mathrm{\mathit{I_{\mathrm{2}}\mathrm{\, =\, }\frac{P}{V_{m}}}}$$

如果𝑎₂是每根导线的横截面积，则每根导线的电阻为：

$$\mathrm{\mathit{R_{\mathrm{2}}\mathrm{\, =\, }\rho \frac{l}{a_{\mathrm{2}}}}}$$

系统中的总功率损耗由下式给出：

$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{2}^{2}}\, R_{\mathrm{2}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{V_{m}} \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{2}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}a_{\mathrm{2}}} }}$$

$$\mathrm{\therefore 横截面积,\mathit{ \: a_{\mathrm{2}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} }}$$

因此，带中点接地的地下两线制直流系统所需的导体材料体积，设为K₁，由下式给出：

$$\mathrm{\mathit{ K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{2}a_{\mathrm{2}}l\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} \right )\times l}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$

比较公式 (1) 和 (2)，我们得到：

$$\mathrm{\mathit{\frac{K_{\mathrm{1}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}{\left (\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}}\mathrm{\, =\, }1}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }K}\: \: \: \cdot \cdot \cdot \left ( 3 \right )}$$

因此，带中点接地的地下两线制直流系统所需的导体材料体积与地下两线制直流系统相同。

地下三线制直流系统所需的导体材料

地下三线制直流系统的电路图如图3所示。在这个系统中，两根外线导线取自发电机的外部端子，中性线取自中点。当平衡负载连接到系统时，中性线中的电流将为零。

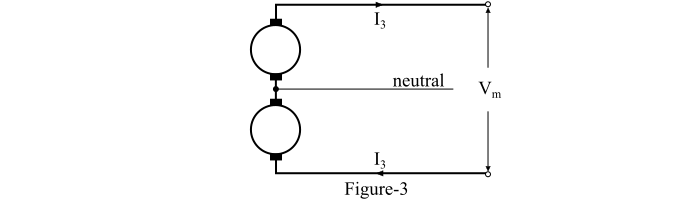
令：

• 𝑉_𝑚 = 外导线间的最大电压

• 𝑃 = 要传输的功率

然后，系统中的负载电流由下式给出：

$$\mathrm{\mathit{I_{\mathrm{3}}\mathrm{\, =\, }\frac{P}{V_{m}}}}$$

此外，如果𝑎₃是每根导线的横截面积，则每根导线的电阻为：

$$\mathrm{\mathit{R_{\mathrm{3}}\mathrm{\, =\, }\rho \frac{l}{a_{\mathrm{3}}}}}$$

因此，系统中的总功率损耗由下式给出：

$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{3}^{2}}\, R_{\mathrm{3}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{V_{m}} \right )^{\mathrm{2}}\times \left (\rho \frac{ \, l}{a_{\mathrm{3}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}a_{\mathrm{3}}} }}$$

$$\mathrm{\therefore 横截面积,\mathit{ \: a_{\mathrm{3}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} }}$$

假设中性线的横截面积是外线导线横截面积的一半。

因此，地下三线制直流系统所需的导体材料体积，设为K₂，由下式给出：

$$\mathrm{\mathit{ K_{\mathrm{2}}\mathrm{\, =\, }\mathrm{2.5}a_{\mathrm{3}}l\mathrm{\, =\, }\mathrm{2.5}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} \right )\times l}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{2}}\mathrm{\, =\, }\frac{\mathrm{5}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 4 \right )}$$

比较公式 (4) 和 (1)，我们得到：

$$\mathrm{\mathit{ \frac{K_{\mathrm{2}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{5}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}{\left ( \frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}}\mathrm{\, =\, }1.25}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{2}}\mathrm{\, =\, }\mathrm{1.25}\times K}\: \: \: \cdot \cdot \cdot \left ( 5 \right )}$$

因此，地下三线制直流系统所需的导体材料体积是地下两线制直流系统所需体积的1.25倍。

Saini Manish Kumar

更新于：2022年2月25日

浏览量：582

开启您的职业生涯

完成课程获得认证

开始学习