架空两相交流输电系统中所需的导体材料

两相交流输电系统

当输电系统由两根线路导线组成，用于将交流电能从发电站传输到变电站进行分配时，称为两相交流输电系统。

根据所用导体的数量，两相交流输电系统分为两种类型，即：

• 两相三线交流系统
• 两相四线交流系统

两相三线交流系统中所需的导体材料

考虑图 1 所示的两相三线交流系统。

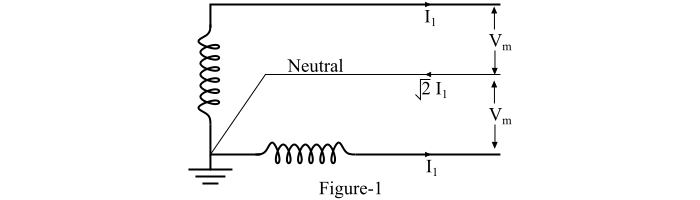
有两根线导体和一根中性线，中性线取自两相绕组的连接点，这两相绕组的电压彼此正交（即 90°）。很明显，每根线导体传输总电力的二分之一。

因此，任何线导体与中性线（即相电压）之间的电压的 RMS 值为：

$$\mathrm{\mathit{V_{ph}\mathrm{\, =\, }\frac{V_{m}}{\sqrt{\mathrm{2}}}}}$$

∴ 每根导体的线电流为：

$$\mathrm{\mathit{I_{\mathrm{1}}\mathrm{\, =\, }\frac{P/\mathrm{2}}{V_{ph}\, \mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{P/\mathrm{2}}{\frac{V_{m}}{\mathrm{\sqrt{2}}}\, \mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{P}{\mathrm{\sqrt{2}}V_{m}\, \mathrm{cos}\, \phi} }}$$

中性线中的电流是线电流的相位和，线导体中的电流彼此相差 90°。

$$\mathrm{\mathit{\therefore \mathrm{中性电流,}I_{n}\mathrm{\, =\, }\sqrt{I_{\mathrm{1}}^{\mathrm{2}}\mathrm{\, +\, }I_{\mathrm{1}}^{\mathrm{2}}}\mathrm{\, =\, }\sqrt{\mathrm{2}}I_{\mathrm{1}}}}$$

假设中性线的横截面积是任一线导体的 √2 倍，以便电流密度保持恒定。

$$\mathrm{\mathit{\therefore \mathrm{中性线电阻,}\, R_{n}\mathrm{\, =\, }\frac{R_{\mathrm{1}}}{\sqrt{\mathrm{2}}}\mathrm{\, =\, }\frac{\rho l}{\sqrt{\mathrm{2}}a_{\mathrm{1}}}}}$$

因此，系统中的总线路损耗由下式给出：

$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I_{\mathrm{1}}^{\mathrm{2}}R_{\mathrm{1}}\mathrm{\, +\, }I_{n}^{\mathrm{2}}R_{n}\mathrm{\, =\, }\mathrm{2}I_{\mathrm{1}}^{\mathrm{2}}R_{\mathrm{1}}\mathrm{\, +\, }\left ( \sqrt{\mathrm{2}}I_{\mathrm{1}} \right )^{\mathrm{2}}\frac{R_{\mathrm{1}}}{\sqrt{\mathrm{2}}}\mathrm{\, =\, }I_{\mathrm{1}}^{\mathrm{2}}R_{\mathrm{1}}\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\left ( \frac{P}{\sqrt{\mathrm{2}}V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho l}{a_{\mathrm{1}}}\right )\times \left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right ) }}$$

$$\mathrm{\mathit{\therefore W\mathrm{\, =\, }\frac{\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )\times P^{\mathrm{2}}\rho l}{\mathrm{2}V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, a_{\mathrm{1}}}}}$$

$$\mathrm{\mathit{\therefore \mathrm{横截面积}, a_{\mathrm{1}}\mathrm{\, =\, }\frac{\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )\times P^{\mathrm{2}}\rho l}{\mathrm{2}\, W\: V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}}$$

因此，两相三线交流系统中所需的导体材料体积（设为 K）由下式给出：

$$\mathrm{\mathit{K\mathrm{\, =\, }\mathrm{2}\, a_{\mathrm{1}}\, l\mathrm{\, +\, }\sqrt{\mathrm{2}}a_{\mathrm{1}}l\mathrm{\, =\, }a_{\mathrm{1}}l\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )}}$$

$$\mathrm{\mathit{\therefore K\mathrm{\, =\, }\frac{\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )^{\mathrm{2}}\times P^{\mathrm{2}}\rho l^{\mathrm{2}}}{\mathrm{2}\, W\: V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }\mathrm{\, =\, }\frac{\mathrm{5.828}\, P^{\mathrm{2}}\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}\: \: \cdot \cdot \cdot \left ( 1 \right )}$$

两相四线交流系统中所需的导体材料

图 2 显示了两相四线交流系统。在这个系统中，四根线导线取自两相绕组的两端，两相绕组的中点连接在一起。

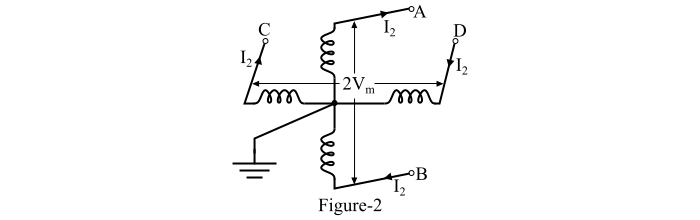
每个相位传输总功率 (P) 的二分之一。现在，考虑两个相位中的一个，例如相位绕组 AB，然后：

$$\mathrm{相位 AB 上的最大电压\, \mathit{AB\mathrm{\, =\, }\mathrm{2}V_{m}}}$$

$$\mathrm{\therefore 相位 AB 上电压的 RMS 值\, \mathit{AB\mathrm{\, =\, }\frac{\mathrm{2}V_{m}}{\mathrm{\sqrt{2}}}\mathrm{\, =\, }\mathrm{\sqrt{2}}V_{m}}}$$

并且，

$$\mathrm{相位 AB 供给的功率（即每相功率）\mathrm{\, =\, }\frac{\mathit{P}}{2}}$$

设 cos 𝜙 为负载的功率因数，则

$$\mathrm{每相负载电流\: \mathit{I_{\mathrm{2}}\mathrm{\, =\, }\frac{P/\mathrm{2}}{\sqrt{\mathrm{2}}\, V_{m}\, \mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{P}{\mathrm{2}\sqrt{\mathrm{2}}\, V_{m}\, \mathrm{cos}\, \phi }}}$$

如果 𝑎₂ 是每根导体的横截面积，R₂ 是每根导体的电阻，则总线路损耗为：

$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{4}\, I_{\mathrm{2}}^{\mathrm{2}}R_{\mathrm{2}}\mathrm{\, =\, }\mathrm{4}\, \times\, \left ( \frac{P}{\mathrm{2\sqrt{2}}V_{m}\, \mathrm{cos}\, \phi} \right )^{\mathrm{2}}\times \frac{\rho l}{a_{\mathrm{2}}} }}$$

$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{P^{\mathrm{2}}\, \rho l}{\mathrm{2}V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, a_{\mathrm{2}}}}}$$

∴ 横截面积为：

$$\mathrm{\mathit{a_{\mathrm{2}}\mathrm{\, =\, }\frac{P^{\mathrm{2}}\, \rho l}{\mathrm{2}W\, V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}}$$

因此，两相四线交流系统中所需的导体材料体积（设为 𝐾₁）由下式给出：

$$\mathrm{\mathit{K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{4}a_{\mathrm{2}}l\mathrm{\, =\, }\mathrm{4}\times \frac{P^{\mathrm{2}}\, \rho l}{\mathrm{2}W\, V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }\times l}}$$

$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, } \frac{\mathrm{2}P^{\mathrm{2}}\, \rho l^{\mathrm{2}}}{W\, V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}\; \; \; \cdot \cdot \cdot \left ( 2 \right )}$$

比较公式 (1) 和 (2)，得到：

$$\mathrm{\mathit{\frac{K_{\mathrm{1}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{2}P^{\mathrm{2}}\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\mathrm{cos^{\mathrm{2}}}\phi } \right )}{\left ( \frac{\mathrm{5.828}P^{\mathrm{2}}\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\mathrm{cos^{\mathrm{2}}}\phi } \right )}\mathrm{\, =\, }\mathrm{0.343}}}$$

$$\mathrm{\therefore \mathit{K_{\mathrm{1}}}\mathrm{\, =\, }0.343\times \mathit{K}\; \; ...\left ( 3 \right )}$$

因此，两相四线制系统中所需的导体材料体积是两相三线制系统所需体积的 0.343 倍。

Manish Kumar Saini

更新于：2022 年 2 月 9 日

463 次浏览

启动您的 职业生涯

通过完成课程获得认证

开始