动力学旋转运动

---

介绍

物体可以进行多种运动，例如平动、旋转、圆周运动、匀速运动等。在旋转运动中，考虑具有确定大小和形状的刚体。物体中存在的粒子围绕固定轴运动呈圆形路径。因此，要理解旋转运动的概念，您必须了解圆周运动。这里的术语以角形式包含。

什么是旋转运动？

如果在物体的角侧（不是在质心）施加力，那么我们会看到物体开始绕固定轴旋转。

在这种类型的运动中，刚体围绕一个固定的点或轴线以圆形路径旋转。物体的各个粒子在任何时间点都以相同的速度一起运动。因此，我们可以说，粒子以相同的角速度进行圆周运动的物体的运动称为旋转运动。

绕固定轴的旋转运动

如果物体中存在的全部粒子都以圆形方式沿着一条直线或固定轴线运动，则会发生旋转运动。物体运动经过的线称为旋转轴。因此，我们可以说，在旋转运动中，物体中的多个粒子围绕固定的旋转轴以圆形形状运动。

旋转加速度

在旋转运动中，所有粒子都沿圆形路径运动。在旋转运动中，每个点的运动方向都在不断变化。由于方向的变化，速度随时间变化，从而产生旋转或角加速度。与平动运动的线性加速度类似，角加速度或旋转加速度定义为粒子角速度变化与所用时间变化的比率。它可以用α表示。

$$\mathrm{\alpha=\frac{d\omega}{dt}}$$

其中ω是角速度，t是所用时间。角加速度的 SI 单位为 rad $\mathrm{s^{-2}}$。其量纲公式为$\mathrm{[M^0 L^0 T^{-2}]}$

扭矩

它也被称为力的旋转类似物。在线性运动中，由于力的作用，物体开始运动，而在旋转运动中，由于扭矩的作用，物体开始围绕一个固定点或轴线旋转或转动。它也可以称为力矩或力的转动效应。

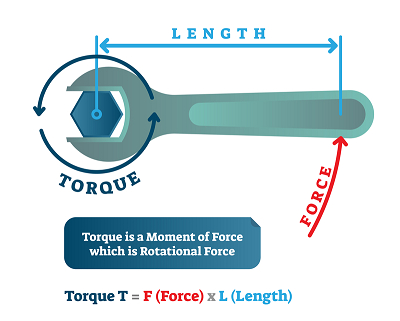
扭矩的测量是力的大小与距旋转点的距离的乘积。

$$\mathrm{扭矩 = 力 \times 垂直距离}$$

其单位为牛顿米 (Nm)。它用希腊字母 τ (tau) 表示。它是一个矢量量。其量纲公式为$\mathrm{[M L^{2} T^{-2}]}$。扭矩的数学表达式由下式给出

$$\mathrm{\overrightarrow{\tau} = \overrightarrow{r} \times \overrightarrow{F}=r Fsin \theta}$$

其中 r 是位置矢量

F 是力的幅度

θ 是位置 r 和力 F 之间的角度

惯性矩

它被称为质量的旋转类似物。线性运动中质量的部分与旋转运动中惯性矩的部分相同。刚体绕给定旋转线或旋转轴的惯性矩，被测量为每个粒子质量与其到旋转轴距离的平方乘积之和。它用 I 表示。

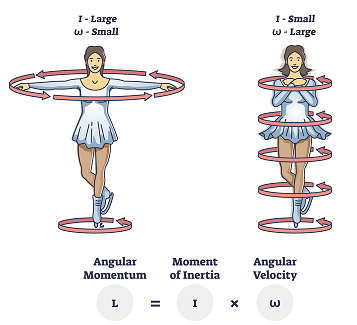
表达式：考虑一个由 n 个粒子组成的物体，其质量为$\mathrm{m_1,m_2,m_3.........m_n}$，距旋转线或旋转轴的距离为$\mathrm{r_1,r_2,r_3,.......r_n}$。然后物体的惯性矩为

$$\mathrm{I=m_1 r_1^{2},m_2 r_2^{2},m_3 r_3^{3},......m_n r_n^{2}}$$

$$\mathrm{I=\displaystyle\sum\limits_{i=1}^n m_ir_i^{2}}$$

惯性矩的 SI 单位为$\mathrm{千克米^{2} (kg\:m^{2})}$。它是一个标量量。其量纲公式为$\mathrm{[ML^{2} T]}$

扭矩(τ) 和惯性矩(I) 之间的关系

让我们考虑一个由 n 个粒子组成的刚体，其质量为$\mathrm{m_1,m_2,m_3............................m_n}$，绕固定轴旋转。设$\mathrm{r_1,r_2,r_3...........................r_n}$分别是粒子的位置。

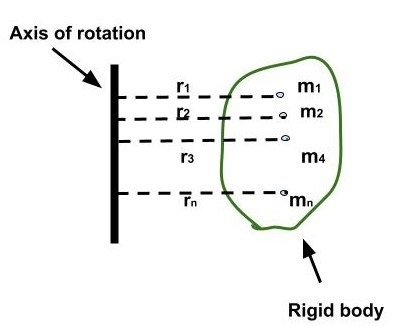
刚体绕轴旋转

因此作用在刚体上的总扭矩为

$$\mathrm{\tau=\tau_1+\tau_2+\tau_3.........\tau_n}$$

$$\mathrm{\tau=F_1 r_1+F_2 r_2+F_3 r_3............F_n r_n}$$

我们知道 F=ma，所以上述方程可以写成

$$\mathrm{\tau= m_1 a_1 r_1+m_2 a_2 r_2+m_3 a_3 r_3............m_n a_n r_n}$$

但是$\mathrm{a=r \alpha}$

$$\mathrm{\tau= m_1 (r_1 \alpha)r_1+m_2 (r_2 \alpha)r_2+m_3 (r_3 \alpha)r_3 .................m_n (r_n \alpha)r_n\:\:\:\:\:\:\:\:\:\:}$$

$$\mathrm{\tau=m_1 r_1^{2} \alpha+m_2 r_2^{2} \alpha+m_3 r_3^{2} \alpha ......................m_n r_n^{2} \alpha\:\:\:\:\:\:\:\:\:\:}$$

$$\mathrm{\tau=(m_1 r_1^{2}+m_2 r_2^{2}+m_3 r_3^{2} .....................m_n r_n^{2})\alpha}$$

$$\mathrm{\tau=\displaystyle\sum\limits_{i=1}^n m_ir_i^{2}\alpha}$$

$\mathrm{\tau=I \alpha}$

$$\mathrm{(\displaystyle\sum\limits_{i=1}^n m_ir_i^{2}=I)}$$

结论

在圆周运动中，物体中的所有粒子都随着时间的推移以不断变化的速度旋转，并产生物体中粒子的角加速度。当对物体施加一对大小相等方向相反的平行力时，就会形成力偶的转动效应。这被称为力偶所施加的扭矩。

常见问题

Q1. 1000 Nm 的恒定扭矩使惯性矩为$\mathrm{100 \:kgm^{2}}$的轮子绕其旋转中心的轴线旋转。求 2 秒内角速度的增量。

答：已知 =1000 Nm，I=200 $\mathrm{kgm^{2}}$

因为$\mathrm{\tau=I \alpha}$

$$\mathrm{\alpha=\frac{\tau}{I}}$$

$$\mathrm{=\frac{1000}{200}=5\:rad/s^{2}}$$

如果 ω 是车轮在 2 秒后的角速度，

$$\mathrm{\omega=\omega_0+\alpha t}$$

$$\mathrm{= 0 + 5 \times 2 = 10 rad/s}$$

Q2. 解释为什么单个力不能平衡扭矩？

答：单个力产生平动，而扭矩产生旋转运动。作用在物体上沿不同作用线的两个大小相等方向相反的平行力的转动效应取决于力偶的力矩或力偶所施加的扭矩。因此，单个力不能平衡扭矩。

Q3. 物体的惯性矩取决于哪些因素？

答：

• 物体的质量，

• 质量绕旋转轴的分布。

Q4. 旋转运动在我们的日常生活中有什么重要意义？

答：旋转运动在车辆和发动机的运动中起着至关重要的作用。直升机的叶片也具有旋转运动。

Q5. 在什么角度下，扭矩最大？

答：当力垂直作用于力臂时。即当$\mathrm{\theta=90^0}$时，扭矩最大。