解释两个有限状态机之间的等价性。
如果两个有限自动机 (FA) 接受输入集 Σ 上的相同字符串集,则称这两个有限自动机等价。
当两个 FA 等价时,存在一个输入集 Σ 上的字符串 x。如果一个 FA 在接受该字符串后到达最终状态,则另一个 FA 也到达最终状态。
方法
下面解释了比较两个 FA 的方法:
令 M 和 M1 为两个 FA,Σ 为输入字符串集。
步骤 1 - 构造一个状态转移表,其中包含成对的条目 (q, q1),其中 q ∈ M 且 q1 ∈ M1,对应每个输入符号。
步骤 2 - 如果我们得到一个对,其中一个为最终状态,另一个为非最终状态,那么我们终止状态转移表的构造,并声明这两个 FA 不等价。
步骤 3 - 当状态转移表中不再出现新的对时,状态转移表的构造终止。
示例
考虑两个确定性有限自动机 (DFA),并检查它们是否等价。
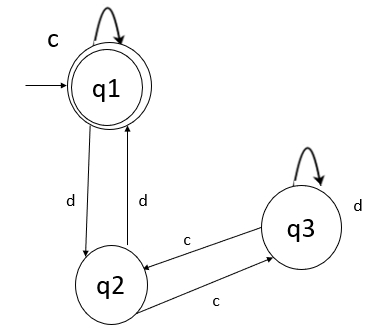
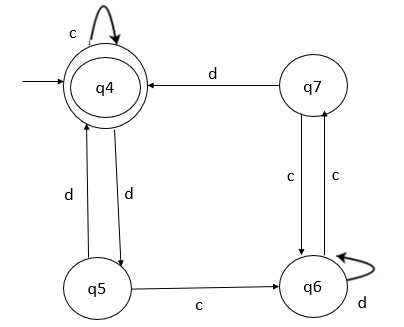
解释
- 步骤 1 - 首先,为每个输入 c 和 d 构造状态转移表。
- 步骤 2 - 从第一个机器 M 在状态 q1 接收输入 c 时,我们仅到达状态 q1,它是最终状态。
- 步骤 3 - 从第二个机器 M1 在状态 q4 接收输入 c 时,我们到达状态 q4,它是最终状态。
- 步骤 4 - 因此,对于输入 c 的状态 (q1, q4),我们得到下一个状态为 (q1, q4)。两者都是最终状态。
- 步骤 5 - 同样,对于状态 (q1, q4) 的输入 d,我们得到下一个状态为 (q2, q5)。两者都是中间状态。因此,两个机器中的第一个状态是相等的。
- 步骤 6 - 同样,我们对两个机器中的其余状态执行此操作。
- 步骤 7 - 在一对状态中,如果两者都是最终状态或两者都是非最终状态,那么我们可以说这两个 DFA 等价,让我们检查其余部分。
状态转移表如下所示:
| 状态 | c | d |
|---|---|---|
| {q1,q4} | {q1, q4} FS FS | {q2, q5} IS IS |
| {q2,q5} | {q3, q6} IS IS | {q1, q4} FS FS |
| {q3, q6} | {q2, q7} IS IS | {q3, q6} IS IS |
| {q2, q7} | {q3, q6} IS IS | {q1, q4} FS FS |
这里,FS 是最终状态,IS 是中间状态。
因此,通过查看上表,很明显我们在一对中没有得到一个最终状态和一个中间状态。因此,我们可以声明这两个 DFA 等价。

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP