数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用中点在 C++ 中查找矩形的角点
假设我们有一个矩形 ABCD，但我们只有中点 P 和 Q 的坐标以及矩形的长度 L。
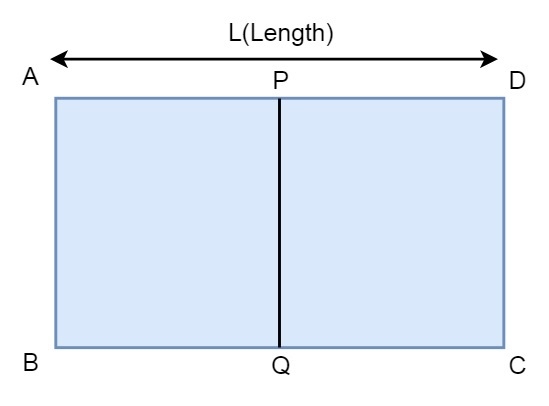
我们的任务是使用 P 和 Q 的坐标以及边长 L 找到 A、B、C 和 D 的坐标。例如，如果 P 是 (1, 0)，Q 是 (1, 2)，L 是 2，则 A、B、C、D 将分别为 (0, 0)、(0, 2)、(2, 2)、(2, 0)。
可能出现三种情况。
- 矩形是水平的，因此 AD 和 BC 平行于 X 轴
- 矩形是垂直的，因此 AD 和 BC 平行于 Y 轴
- 矩形与轴成一定角度。
对于第三种情况，我们必须使用 P 和 Q 的坐标找到斜率。如果我们得到 AD 的斜率，那么我们就可以生成通过 AD 的直线方程，然后使用距离公式得到结果。
$$AD 的斜率，m=\frac{px-qx}{py-qy}$$ $$沿 x 轴的位移，dx=\frac{L}{2\sqrt{1+m^{2}}}$$ $$沿 y 轴的位移，dy=\frac{mL}{2\sqrt{1+m^{2}}}$$
示例
#include <iostream>
#include <cmath>
using namespace std;
class Point {
public:
float x, y;
Point(float a = 0.0f, float b = 0.0f) {
x = a, y = b;
}
};
void printCorners(Point p, Point q, float l) {
Point a, b, c, d;
if (p.x == q.x) {
a.x = p.x - (l/2.0);
d.x = p.x + (l/2.0);
a.y = d.y = p.y;
b.x = q.x - (l/2.0);
c.x = q.x + (l/2.0);
b.y = c.y = q.y;
}else if (p.y == q.y) {
a.y = p.y - (l/2.0);
d.y = p.y + (l/2.0);
a.x = d.x = p.x;
b.y = q.y - (l/2.0);
c.y = q.y + (l/2.0);
b.x = c.x = q.x;
}else{
float m = (p.x-q.x)/float(q.y-p.y);
float dx = (l /sqrt(1+(m*m))) *0.5 ;
float dy = m*dx;
a.x = p.x - dx;
a.y = p.y - dy;
d.x = p.x + dx;
d.y = p.y + dy;
b.x = q.x - dx;
b.y = q.y - dy;
c.x = q.x + dx;
c.y = q.y + dy;
}
cout << "A (" << a.x << ", " << a.y << ")\n"
<< "B (" << b.x << ", " << b.y << ")\n"
<< "C (" << c.x << ", " << c.y << ")\n"
<< "D (" << d.x << ", " << d.y << ")\n";
}
int main() {
Point p(1, 1), q(-1, -1);
printCorners(p, q, 2*sqrt(2));
}输出
A (0, 2) B (-2, 0) C (0, -2) D (2, 0)
更新于: 2019年10月21日
132 次查看
广告